量子相位估计的应用:求解幺正变换的平方根
Ping Zhou, 2021-08-27
在前文《量子相位估计》里,我们讨论了量子相位估计算法,它也是很多量子算法能有指数级加速的关键。今天来讨论量子相位估计的另一个应用:求解给定幺正变换的平方根。
假如我们有一个幺正变换 \(U\) ,求解它的k次方 \(U^k\) 很容易,只要把k个 \(U\) 连起来就行,但是如果要求它的平方根 \(U^{1/2}\) 呢?事情就没那么简单了。今天来讨论一下,如何利用量子相位估计来求给定幺正变换的平方根,或者说,构造一个新的幺正变换,使它的平方等于给定的幺正变换。
先回顾一下什么是量子相位估计。
假如我们有一个幺正算符 \(U\) , \(|u\rangle\) 是它的一个本征矢量,对应的本征值是 \(e^{i\phi}\) ( \(\phi\) 在0到 \(2\pi\) 之间):
\begin{matrix} U|u\rangle = e^{i\phi}|u\rangle \end{matrix}“量子相位估计”问题,就是从幺正算符 \(U\) 和 \(|u\rangle\) ,估算相应的本征值 \(e^{i\phi}\) 里的相位 \(\phi\) 。
量子相位估计的电路如下,输入 \(|u\rangle\) 是U的一个本征向量,在输出端测量,就能得到其本征值的相位 \(\psi=\phi/2\pi\) 的 n位二进制近似 。
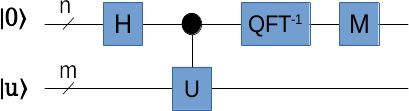
你可能注意到,这里的输入 \(|u\rangle\) 是U的 一个 本征向量。但是,U可能有很多个本征向量,对不对?
如果这个相位估计电路输入的不是某一个本征向量,而是U所有本征向量的叠加呢?右边输出会得到什么?也就是说,如果左边的输入是U的所有本征向量 \(|u_j\rangle\) 的叠加:
\begin{matrix} |\psi\rangle = \sum_j \alpha_j |u_j\rangle \end{matrix}猜猜右边会得到啥?
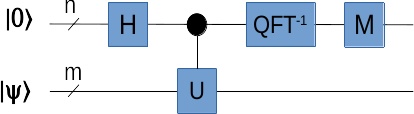
答案很容易猜到,既然左边的输入是本征向量的叠加,那么右边的输出,就是对应的相位估计结果的叠加:
\begin{matrix} U|\psi\rangle = \sum_j \alpha_j e^{i\phi_j} |u_j\rangle \end{matrix}也就是说,如果在右边测量,会得到某一个本征向量 \(|u_j\rangle\) 的相位估计,其概率取决于它在输入的叠加态里的强度 \(|\alpha_i|^2\) 。
回到求U的平方根问题。
什么是『U的平方根』?显然,这个变换的平方是U。根据前面的假设,U会给它的每个本征向量 \(|u_j\rangle\) 加上各自的相位 \(\phi_j\) :
\begin{matrix} U|u_j\rangle = e^{i\phi_j}|u\rangle \end{matrix}那么如果我们能构造一个变换,比如我们称它为V,使得它对每个本征向量 \(|u_j\rangle\) 有这样的效果:
\begin{matrix} V|u_j\rangle = e^{i\phi_j / 2}|u\rangle \end{matrix}这个V变换给各个本征向量加上的相位,是U的一半,那么这个V变换的平方,不就是U了?
\begin{matrix} V^2 |u_j\rangle = VV|u_j\rangle = e^{i\phi_j}|u\rangle = U|u_j\rangle \end{matrix}所以, \(V=U^{1/2}\) 。我们的目标就是从U出发,构造这样的一个变换V出来。
下面这个电路,就是利用量子相位估计来求解U的平方根:

其中, \(|\psi\rangle\) 是U的所有本征向量的叠加:
\begin{matrix} |\psi\rangle = \sum_j \alpha_j |u_j\rangle \\ U|\psi\rangle = \sum_j \alpha_j e^{i\phi_j} |u_j\rangle \end{matrix}分析一下原理。
在t1时刻,我们对U的所有本征向量 \(|u_j\rangle\) 做了相位估计。
因为 \(|\phi_j\rangle\) 是0到 \(2\pi\) 之间的角度,把它除以 \(2\pi\) 后,可以表示成0到1之间的小数 \(\theta_j = \frac{\phi_j} {2\pi}\) 。量子相位估计得到的就是各个 \(\theta_j\) 的n位二进制估计。
如果我们把 \(\theta_j\) 看成是二进制小数 \(0.a_1a_2 \dots a_n\) ,并把第一个寄存器的状态看作n位二进制数 \(a_1a_2 \dots a_n\) 的话,它其实就是 \(\theta_j\) 右移n位: \(2^n \theta_j = 2^n \frac{\phi_j}{2\pi}\) 。第二个寄存器仍然是 \(|u_j\rangle\) 。
所以,t1时刻的(近似)状态是:
\begin{matrix} t1: \sum_j \alpha_j |2^n \theta_j\rangle |u_j\rangle = \sum_j \alpha_j |\frac{2^n \phi_j} {2\pi} \rangle |u_j\rangle \end{matrix}接下来,我们制备这样一个受控旋转门R:
\begin{matrix} R|y\rangle = e^{i \frac{\pi y}{2^n}}|y\rangle \end{matrix}这个受控旋转门R,根据输入的n个量子位的状态(看作n位二进制数y),给它加上 \(\frac{\pi y}{2^n}\) 的相位。
这个R门,作用于t1时刻里的状态 \(|\frac{2^n\phi_j}{2\pi}\rangle\) 的话(即 \(y=\frac{2^n\phi_j}{2\pi}\) ):
\begin{matrix} R|\frac{2^n\phi_j}{2\pi}\rangle = e^{i\pi \frac{2^n\phi_j}{2\pi} / 2^n} |\frac{2^n\phi_j}{2\pi}\rangle \\ = e^{i \frac{\phi_j}{2}} |\frac{2^n\phi_j}{2\pi}\rangle \end{matrix}看到没有?我们利用这个受控旋转门R,达到了把相位减半的目的( \(\phi_j / 2\) )!
所以在t2时刻,系统的状态是这样:
\begin{matrix} t2: \sum_j \alpha_j e^{i\phi_j / 2} |\frac{2^n \phi_j}{2\pi}\rangle |u_j\rangle \end{matrix}这个状态看起来已经接近我们想要的 \(V=U^{1/2}\) 变换了?
但是别忘了,要实现一个完整的 \(U^{1/2}\) 变换,还需要恢复输入状态,否则的话,没法像U那样作重复变换。
这个『恢复』的意思是,需要在输出端恢复到和U类似的状态,即第一个寄存器在变换后应该恢复到 \(|0\rangle\) 的状态。而前面做的相位估计,计算的结果在第一个寄存器里,我们需要把这个相位估计计算『回滚』(uncompute),从而恢复第一个寄存器的状态。
要达到这个目的,我们其实只需要做一个相位估计的逆变换就行了,就是电路图中的右半部分:
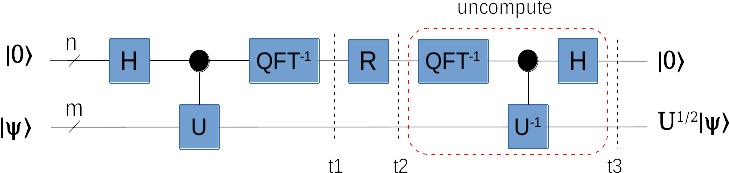
经过这个uncompute过程,t3时刻的状态:
\begin{matrix} t3: \sum_j \alpha_j e^{i\phi_j / 2} |0\rangle |u_j\rangle = |0\rangle U^{1/2} |u_j\rangle \end{matrix}这就是我们要的U的平方根 \(U^{1/2}\) 。
感谢阅读!