假如我们有一个幺正算符 \(U\) ，他的本征矢量是 \(|u\rangle\) ，本征值是 \(e^{i\phi}\) （ \(\phi\) 在0到 \(2\pi\) 之间）。

“量子相位估计“问题，就是从幺正算符 \(U\) 和它的本征矢量 \(|u\rangle\) ，估算它的本征值 \(e^{i\phi}\) 里的相位 \(\phi\) ：

Estimate phase \(\phi\) of an eigenvalue of an unitary operator \(U\), given its eigenvector \(|u\rangle\).

既然幺正算符 \(U\) 的本征矢量是 \(|u\rangle\) ，并且其对应的本征值是 \(e^{i\phi}\) ，那么根据本征矢量的定义：

\begin{matrix} U|u\rangle = e^{i\phi}|u\rangle \end{matrix}

那么如果对 \(|u\rangle\) 进行多次U变换，不难推导出：

\begin{matrix} U^k|u\rangle = e^{ik\phi}|u\rangle \end{matrix}

所以多次对 \(|u\rangle\) 进行 \(U\) 变换，得到的状态仍然是 \(|u\rangle\) ，只不过给它增加了一个全局相位。

我们可以从 \(U\) 制备出一组（n个）这样的幺正变换： \(U, U^2, U^4, U^8, \dots, U^{2^{n-1}}\)

然后，对这些幺正变换作一些扩展，给它们加上控制输入，变成类似CNOT这样的可控 \(U^{2^k}\) 变换（也就是当控制输入是 \(|1\rangle\) 的时候才进行 \(U^{2^k}\) 变换）：

\begin{matrix} CU, CU^2, CU^4, CU^8, \dots, CU^{2^{n-1}} \end{matrix}

再把这些可控U变换这样接起来：

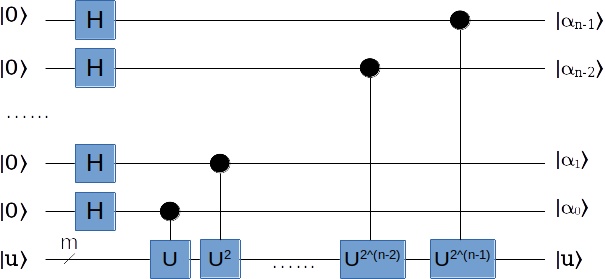
右边会是什么状态？我们来推导一下。

从这个电路图可以看出，实际上每一步是用输入中的一位作为控制输入，对 \(|u\rangle\) 作可控U变换。

例如在第k步，使用第k个量子位作为控制输入，输入状态是： \(\frac{1}{\sqrt 2}(|0\rangle + |1\rangle)|u\rangle\)

第k位对应的可控U变换是 \(CU^{2^{k}}\) ，经过这个可控U变换后，状态变成了：

\begin{matrix} CU^{2^{k}} \frac{1}{\sqrt 2}(|0\rangle + |1\rangle) \\ = \frac{1}{\sqrt 2}(|0\rangle|u\rangle + |1\rangle U^{2^k}|u\rangle) \\ = \frac{1}{\sqrt 2}(|0\rangle|u\rangle + |1\rangle e^{i2^k\phi}|u\rangle) \\ = \frac{1}{\sqrt 2}(|0\rangle + e^{i2^k\phi}|1\rangle) |u\rangle \\ \end{matrix}

所以经过这一系列的可控U变换，右边的各个量子位状态变成了这样：

\begin{matrix} |\alpha_0\rangle = \frac{1}{\sqrt 2}(|0\rangle + e^{i\phi}|1\rangle) \\ |\alpha_1\rangle = \frac{1}{\sqrt 2}(|0\rangle + e^{i2\phi}|1\rangle) \\ |\alpha_2\rangle = \frac{1}{\sqrt 2}(|0\rangle + e^{i2^2\phi}|1\rangle) \\ \dots \\ |\alpha_k\rangle = \frac{1}{\sqrt 2}(|0\rangle + e^{i2^k\phi}|1\rangle) \\ \dots \\ |\alpha_{n-1}\rangle = \frac{1}{\sqrt 2}(|0\rangle + e^{i2^{n-1}\phi}|1\rangle) \\ \end{matrix}

这里的 \(\phi\) 是一个角度，我们可以把它写成 \(\phi=2\pi \psi\) ，显然这里的 \(\psi\) 只用考虑小数部分，整数部分可以忽略，所以我们进一步假设 \(\psi\) 可以近似成n位的二进制小数：

\(\psi=0.\psi_1\psi_2\dots\psi_n\)

把这个代入到前面的式子里去，其中的第k位， \(|1\rangle\) 的相位要乘以 \(2^k\) ，也就是小数点向右移动k位，同样，移位后的整数部分可以忽略：

\begin{matrix} e^{i 2^k \phi} = e^{2\pi i 2^k 0.\psi_1\psi_2\dots\psi_n} \\ = e^{2\pi i \psi_1\psi_2\dots\psi_k.\psi_{k+1}\dots\psi_n} \\ = e^{2\pi i 0.\psi_{k+1}\dots\psi_n} \\ \end{matrix}

所以，电路右边的状态，用 \(\psi\) 表示的话是这样的：

\begin{matrix} |\alpha_0\rangle = \frac{1}{\sqrt 2}(|0\rangle + e^{2\pi i 0.\psi_1\psi_2\dots\psi_n}|1\rangle) \\ |\alpha_1\rangle = \frac{1}{\sqrt 2}(|0\rangle + e^{2\pi i 0.\psi_2\psi_3\dots\psi_n}|1\rangle) \\ |\alpha_2\rangle = \frac{1}{\sqrt 2}(|0\rangle + e^{2\pi i 0.\psi_3\psi_4\dots\psi_n}|1\rangle) \\ \dots \\ |\alpha_{n-2}\rangle = \frac{1}{\sqrt 2}(|0\rangle + e^{2\pi i 0.\psi_{n-1}\psi_n}|1\rangle) \\ |\alpha_n\rangle = \frac{1}{\sqrt 2}(|0\rangle + e^{2\pi i 0.\psi_n}|1\rangle) \\ \end{matrix}

如果您还记得之前量子傅里叶变换的输入输出解读的话，就会发现：这正是 \(\psi\) 的n位量子傅里叶变换的输出啊！

那么，如果在这后面再接上一个量子傅立叶逆变换，不就能回到 \(\psi\) （也就是 \(\phi\) ）了？

完整的量子相位估计电路：

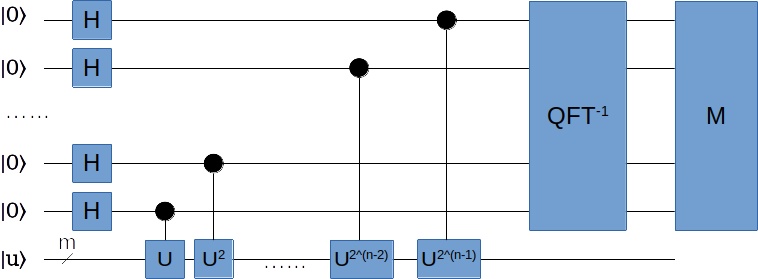
总结一下，这个“量子相位估计”电路的作用，就是对给定的幺正变换 \(U\) 和它的本征矢量 \(|u\rangle\) ，给出其本征值的相位 \(\psi=\phi/2\pi\) 的 n位二进制近似 。

其实…之前的量子因式分解Shor算法就可以看作是量子相位估计的一个应用。

回想一下，Shor算法的实现里，使用的“指数取模”变换 \(U_f\) ，其内部实现其实是一系列的“乘法取模”变换（这里略去了辅助量子位）：

\begin{matrix} U|x\rangle = |ax \mod N\rangle \end{matrix}

可以证明，下面这一系列矢量都是这个变换 \(U\) 的本征矢量（其中r是a对N的order，即 \(a^r=1 \mod N\) ）：

\begin{matrix} |u_s\rangle = \frac{1}{\sqrt r} \sum_{k=0}^{r-1} e^{-\frac{2\pi isk}{r}} |a^k \mod N\rangle \\ (0 \le s \le r-1) \end{matrix}

而它们各自对应的本征值，则是 \(e^{\frac{2\pi is}{r}}\) ，换句话说：

\begin{matrix} U|u_s\rangle = e^{\frac{2\pi is}{r}} |u_s\rangle \end{matrix}

证明过程这里先略过，后面有空再补，或者您可以作为练习自行推导 :-)

我们看Shor算法里面实现“指数取模”的方法，以及后面作的量子傅立叶变换，是不是就是相当于对这个U的本征值做了一个量子相位估计？

根据估计出来的相位 \(\frac{2\pi s}{r}\) ，我们得到分数 \(\frac{s}{r}\) 的一个近似，然后再用连分数算法，估算出r的值，也就是要找的order。

所以，Shor算法里的order finding其实就是量子相位估计的一个应用。

感谢阅读！