量子傅里叶变换详解 (1) 输入输出解读
Ping Zhou, 2021-05-17
之前的Shor算法系列,讲了利用量子傅立叶变换QFT来提取函数周期信息。这次歪个楼,聊聊量子傅立叶变换。
假如我们用n个量子位搭了一个QFT电路(后文会讲到如何实现),如何解读它的输入和输出呢?
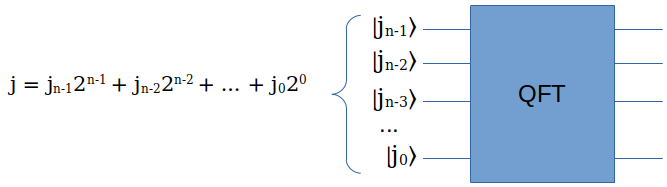
假设我们的电路输入状态是某个基态 \(|j\rangle\) ,它是由n个量子位组成的,我们把它展开成二进制表示的话:
\begin{matrix} |j\rangle = |j_{n-1}j_{n-2}\dots j_0\rangle \\\ j = j_{n-1}2^{n-1} + j_{n-2}2^{n-2} + \dots + j_0 2^0 \end{matrix}经过QFT,我们得到一个新的状态:
\begin{matrix} QFT|j\rangle = \frac{1}{\sqrt{2^n-1}} \sum_{k=0}^{2^n-1} \omega^{jk} |k\rangle \\\ = \frac{1}{\sqrt{2^n}} \sum_{k=0}^{2^n-1} e^{2\pi ijk/2^n} |k\rangle \end{matrix}其中每个分量k的相位 \(e^{2\pi ijk/2^n}\) 。而因为其中的 \(k\) 也是一个n位二进制数,也就是说:
\begin{matrix} k = k_{n-1}2^{n-1} + k_{n-2}2^{n-2} + \dots + k_0 2^0 \end{matrix}那么这个相位里,是把k除以 \(2^n\) ,我们把k的二进制展开代入进去就变成了这样:
\begin{matrix} k / 2^n = \frac{k_{n-1}}{2^1} + \frac{k_{n-2}}{2^2} + \dots + \frac{k_0}{2^n} \end{matrix}等一下,这个式子是不是似曾相识?
这不就是二进制小数点表示嘛!
\begin{matrix} k / 2^n = 0.k_{n-1}k_{n-2}\dots k_0 = \sum_{l=1}^n \frac{k_{n-l}}{2^l} \end{matrix}所以,QFT后的状态,可以写成这样:
\begin{matrix} QFT|j\rangle = \frac{1}{\sqrt{2^n}} \sum_{k=0}^{2^n-1} e^{2\pi ijk/2^n} |k\rangle \\\ = \frac{1}{\sqrt{2^n}} \sum_{k=0}^{2^n-1} e^{2\pi ij \sum_{l=1}^n \frac{k_{n-l}}{2^l}} |k_{n-1}k_{n-2}\dots k_0\rangle \end{matrix}进一步分析, \(\sum_{k=0}^{2^n-1}(\dots)\) 这东西,就是用 k 把n位二进制数全部遍历一遍。如果我们看 k 的二进制数表示,它的每一位可能的选择是0和1,这样的遍历其实就是把每一位的0/1选择都遍历一遍。所以这个求和也可以展开成:
\begin{matrix} \sum_{k=0}^{2^n-1} (\dots)= \sum_{k_{n-1}=0}^1 \sum_{k_{n-2}=0}^1 \dots \sum_{k_0=0}^1 (\dots) \end{matrix}好,接下来看后面的东西。
\(e^{2\pi ij \sum_{l=1}^n \frac{k_{n-l}}{2^l}} |k_{n-1}k_{n-2}\dots k_0\rangle\) 是n个量子位,它们的相位是指数之和,把它们分别展开:
\begin{matrix} e^{2\pi ij \sum_{l=1}^n \frac{k_{n-l}}{2^l}} |k_{n-1}k_{n-2}\dots k_0\rangle = \\\ = e^{2\pi ij \frac{k_{n-1}}{2^1}} e^{2\pi ij \frac{k_{n-2}}{2^2}} \dots e^{2\pi ij \frac{k_{0}}{2^n}} |k_{n-1}\rangle |k_{n-2}\rangle \dots |k_0\rangle \\\ = \left( e^{2\pi ij \frac{k_{n-1}}{2^1}}|k_{n-1}\rangle \right) \otimes \left( e^{2\pi ij \frac{k_{n-2}}{2^2}}|k_{n-2}\rangle \right) \otimes \dots \otimes \left( e^{2\pi ij \frac{k_{0}}{2^n}}|k_0\rangle \right) \\\ = \otimes_{l=1}^n \left( e^{2\pi ij \frac{k_{n-l}}{2^l}}|k_{n-l}\rangle \right) \end{matrix}前后两个式子合起来:
\begin{matrix} QFT|j\rangle = \\\ \frac{1}{\sqrt{2^n}} \sum_{k_{n-1}=0}^1 \dots \sum_{k_0=0}^1 \left[\otimes_{l=1}^n e^{2\pi ij \frac{k_{n-l}}{2^l}} |k_{n-l}\rangle\right] \end{matrix}我们注意到,这个式子的前面一串求和,其实也是对 \(k_{n-l}\) 的遍历( \(l\) 从1到n),所以这个式子里的 \(\otimes_{l=0}^n\) 可以提到前面去,变成:
\begin{matrix} QFT|j\rangle = \\\ \frac{1}{\sqrt{2^n}} \sum_{k_{n-1}=0}^1 \dots \sum_{k_0=0}^1 \left[\otimes_{l=1}^n e^{2\pi ij \frac{k_{n-l}}{2^l}} |k_{n-l}\rangle\right] & (1)\\\ = \frac{1}{\sqrt{2^n}} \otimes_{l=1}^n \left[ \sum_{k_{n-l}=0}^1 e^{2\pi ij \frac{k_{n-l}}{2^l}} |k_{n-l}\rangle \right] & (2) \\\ \end{matrix}车速有点快?我们来验证一下上面两个式子(1)和(2)是等价的。
(1)前面的一串求和,是对n位二进制数的遍历,k从 0 到 \(2^n-1\) ,每次确定一个n位二进制数k,送到 \(\otimes\) 里去,出来一个n位量子位组成的状态,这样搞 \(2^n\) 次,最后把遍历的结果叠加起来。
所以(1)的结果,是n个量子位所有 \(2^n\) 个状态的叠加:
\begin{matrix} |0\rangle & = |00\dots00_2\rangle \\\ |1\rangle & = |00\dots01_2\rangle \\\ |2\rangle & = |00\dots10_2\rangle \\\ |3\rangle & = |00\dots11_2\rangle \\\ \dots & \dots \\\ |2^n-1\rangle & = |11\dots11_2\rangle \\\ \end{matrix}而其中每个状态的 相位 ,取决于该状态下各个量子位的0/1状态,即 \(e^{2\pi ij \frac{k_{n-1}}{2^1}} e^{2\pi ij \frac{k_{n-2}}{2^2}} \dots e^{2\pi ij \frac{k_{0}}{2^n}}\) (左边是状态,右边是它的相位):
\begin{matrix} |00\dots00_2\rangle & e^{2\pi ij \frac{0}{2^1}} e^{2\pi ij \frac{0}{2^2}} \dots e^{2\pi ij \frac{0}{2^(n-1)}} e^{2\pi ij \frac{0}{2^n}} \\\ |00\dots01_2\rangle & e^{2\pi ij \frac{0}{2^1}} e^{2\pi ij \frac{0}{2^2}} \dots e^{2\pi ij \frac{0}{2^(n-1)}} e^{2\pi ij \frac{1}{2^n}} \\\ |00\dots10_2\rangle & e^{2\pi ij \frac{0}{2^1}} e^{2\pi ij \frac{0}{2^2}} \dots e^{2\pi ij \frac{1}{2^(n-1)}} e^{2\pi ij \frac{0}{2^n}} \\\ |00\dots11_2\rangle & e^{2\pi ij \frac{0}{2^1}} e^{2\pi ij \frac{0}{2^2}} \dots e^{2\pi ij \frac{1}{2^(n-1)}} e^{2\pi ij \frac{1}{2^n}} \\\ \dots & \dots \\\ \end{matrix}在(2)中, \(\otimes\) 被提到了前面,变成遍历每个量子位,然后对每个量子位,遍历它的两个基态的相位:
\begin{matrix} l=1: & (k_{n-1}) & \left[ e^{2\pi ij \frac{0}{2^1}}|0\rangle + e^{2\pi ij \frac{1}{2^1}}|1\rangle \right] \\\ l=2: & (k_{n-2}) & \left[ e^{2\pi ij \frac{0}{2^2}}|0\rangle + e^{2\pi ij \frac{1}{2^2}}|1\rangle \right] \\\ l=3: & (k_{n-3}) & \left[ e^{2\pi ij \frac{0}{2^3}}|0\rangle + e^{2\pi ij \frac{1}{2^3}}|1\rangle \right] \\\ \dots && \\\ l=n: & (k_{0}) & \left[ e^{2\pi ij \frac{0}{2^n}}|0\rangle + e^{2\pi ij \frac{1}{2^n}}|1\rangle \right] \\\ \end{matrix}这一串方括号里的东西乘起来(其实是张量积),就是对所有n个量子位的状态的张量积:
- 每个方括号里有2项,n个方括号相乘,一共产生 \(2^n\) 项;
- 乘出来的每一项都是n位量子位组成的状态,而它的相位就是各个量子位的相位的乘积。
还是从简单的例子看,例如2个量子位:
\begin{matrix} (\alpha_0|0\rangle + \beta_0|1\rangle) \otimes (\alpha_1|0\rangle + \beta_1|1\rangle) = \\\ \alpha_0\alpha_1|00\rangle + \alpha_0\beta_1|01\rangle + \beta_0\alpha_1|10\rangle + \beta_0\beta_1|11\rangle \\\ \end{matrix}这可不就是(1)的结果?所以(1)和(2)是等价的。
好,继续往下推导:
\begin{matrix} QFT|j\rangle = & \\\ \frac{1}{\sqrt{2^n}} \otimes_{l=1}^n \left[ \sum_{k_{n-l}=0}^1 e^{2\pi ij \frac{k_{n-l}}{2^l}} |k_{n-l}\rangle \right] & (2) \\\ \end{matrix}方括号里的东西,其实就2项, \(k_{n-l}=0\) 和 \(k_{n-l}=1\) 。如果 \(k_{n-l}=0\) ,那么相位就是 \(e^0=1\) ;反之如果 \(k_{n-l}=1\) ,那么相位就是 \(e^{2\pi ij \frac{1}{2^l}}\) 。所以所以(2)可以展开成这样:
\begin{matrix} \frac{1}{\sqrt{2^n}} \otimes_{l=1}^n \left[ \sum_{k_{n-l}=0}^1 e^{2\pi ij \frac{k_{n-l}}{2^l}} |k_{n-l}\rangle \right] & (2) \\\ = \frac{1}{\sqrt{2^n}} \otimes_{l=1}^n \left[ |0\rangle + e^{2\pi ij/2^l} |1\rangle \right] & (3) \\\ \end{matrix}每个方括号里的 \(|1\rangle\) ,相位是 \(e^{2\pi i j/2^l}\) ,没有了k,剩下 \(j, l\) 。
然后我们看 \(j/2^l\) 这个东西, \(j\) 本身也是个n位二进制数 \(j=j_{n-1}j_{n-2}\dots j_0\) ,那么它除以 \(2^l\) 后,就变成了:
\begin{matrix} j/2^l = \frac{j_{n-1}2^{n-1} + j_{n-2}2^{n-2} + \dots + j_02^0}{2^l} \\\ = j_{n-1}2^{n-1-l} + j_{n-2}2^{n-2-l} + \dots + j_0 2^{-l} \end{matrix}从二进制数的角度看,相当于把小数点向左移了 \(l\) 位:
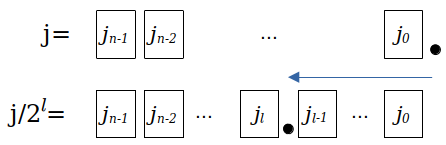
很明显这是个带小数点的二进制数:前面的 \(n-l\) 项是整数部分,而后面的 \(l\) 项是小数部分。
而这个数放到 \(e^{2\pi i}\) 的指数上,整数部分是可以全部消掉的(还记得 \(e^{2\pi i k} = 1\) 吗?),只剩下小数点部分:
\begin{matrix} e^{2\pi ij/2^l} = e^{2\pi i 0.j_{l-1}j_{l-2}\dots j_{0}} \end{matrix}所以前面的(3)可以扩展成:
\begin{matrix} QFT|j\rangle = & \\\ \frac{1}{\sqrt{2^n}} \otimes_{l=1}^n \left[ |0\rangle + e^{2\pi ij/2^l} |1\rangle \right] & (3) \\\ = \frac{1}{\sqrt{2^n}} \left( |0\rangle + e^{2\pi i 0.j_0}|1\rangle \right) \left( |0\rangle + e^{2\pi i 0.j_1j_0}|1\rangle \right) \dots \left( |0\rangle + e^{2\pi i 0.j_{n-1}j_{n-2}\dots j_0}|1\rangle \right) & \\\ \end{matrix}这个结论很重要,可以看作是量子傅立叶变换的定义!