要理解Grover算法的原理，最直观的方法是把它图像化，从几何意义来理解。

回顾一下上文的量子搜索电路：

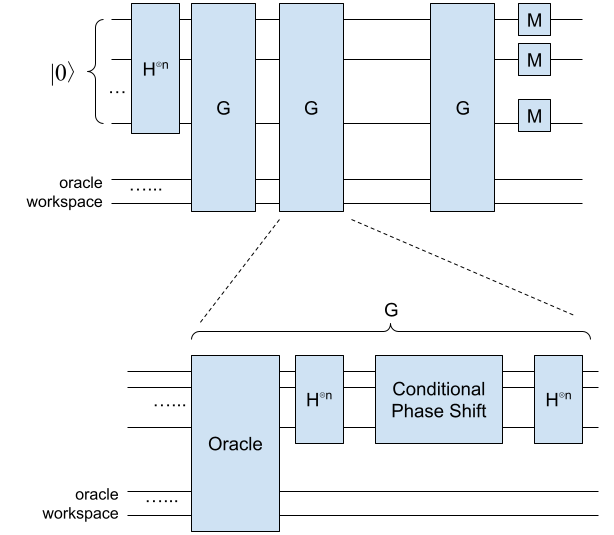
我们的电路有n个搜索用的量子比特，可以表示\(N=2^{n}\)个基态，对应搜索空间0到N-1的编号。为方便讨论，我们用\(|0\rangle, |1\rangle, |2\rangle, |3\rangle, \dots, |N-1\rangle\)来表示这些基态。

假定在这N个编号中，有M个是符合条件的答案。在上文的讨论中我们假定M=1，也就是只有1个符合条件的编号，这里我们把它扩展到更普遍的情况，M可以大于1，也就是可以有多个符合条件的答案。因此不符合条件（也就是让判断函数f返回0）的编号有N-M个。

我们把所有 不符合条件 的N-M个基态叠加在一起，组成一个叠加态的状态向量，把它记作\(|\alpha\rangle\)。

类似的，把所有 符合条件 的M个状态叠加在一起，组成一个状态向量，把它记作\(|\beta\rangle\)。

显然，上面这两个向量\(|\alpha\rangle\)，\(|\beta\rangle\)是正交的。因此我们可以用它们作轴，张成一个二维平面。

然后我们在这个平面里，考察前面G变换公式里的\(|\psi\rangle\)，这是一个所有基态无差别叠加的状态，那么这个\(|\psi\rangle\)在这个二维平面里，可以写成：

\begin{matrix} |\psi\rangle=\sqrt{\frac{N-M}{N}}|\alpha\rangle + \sqrt{\frac{M}{N}}|\beta\rangle \end{matrix}

这个\(|\psi\rangle\)向量，和\(|\alpha\rangle\)轴之间的夹角，我们记作\(\frac{\theta}{2}\)，如下图所示：

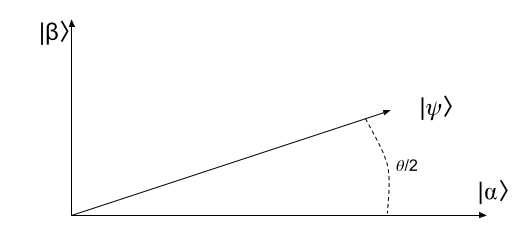
根据简单的三角函数，我们很容易得到：

\begin{matrix} \cos\frac{\theta}{2} = \sqrt{\frac{N-M}{N}} && \sin\frac{\theta}{2} = \sqrt{\frac{M}{N}} \end{matrix}

继续分析G变换。从上文我们知道，G变换可以写成：

\[ G=(2|\psi\rangle \langle\psi|-I)O \]

我们先从O（Oracle）变换看起。O变换干了什么呢？它是把输入的状态\(|x\rangle\)变成\((-1)^{f(x)} |x\rangle\)。如果f(x)=1，那么它就给输出加上一个-1的相位，否则不变。那么这个操作在二维平面图中，实际上就是把输入的向量对\(|\alpha\rangle\)轴做了一个 反射 。

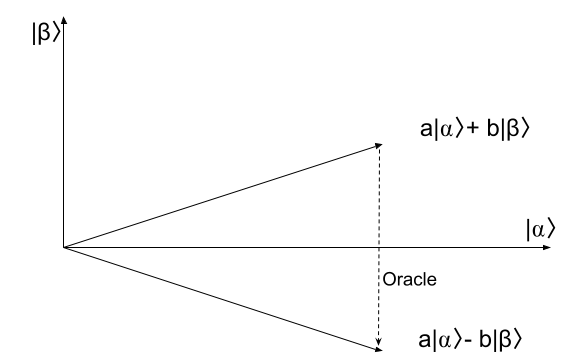
所以，Oracle变换的作用，就是把输入向量对\(|\alpha\rangle\)轴做一个反射。

然后继续看G变换后面的部分，\(2|\psi\rangle\langle\psi|-I\)，其中\(|\psi\rangle\)是所有基态的无差别叠加态。这个变换的效果是什么呢？我们来简单推导一下：

\begin{matrix} |\psi\rangle\langle\psi|= \begin{bmatrix} \frac{1}{\sqrt{N}} \\ \frac{1}{\sqrt{N}} \\ \vdots \\ \frac{1}{\sqrt{N}} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{N}} && \frac{1}{\sqrt{N}} && \dots && \frac{1}{\sqrt{N}} \end{bmatrix} \\ = \begin{bmatrix} \frac{1}{N} && \frac{1}{N} && \dots && \frac{1}{N} \\ \vdots && && && \vdots \\ \frac{1}{N} && \frac{1}{N} && \dots && \frac{1}{N} \end{bmatrix} \end{matrix}

因此：

\begin{matrix} 2|\psi\rangle\langle\psi|-I = \begin{bmatrix} (\frac{2}{N}-1) && \frac{2}{N} && \frac{2}{N} && \dots && \frac{2}{N} \\ \frac{2}{N} && (\frac{2}{N}-1) && \frac{2}{N} && \dots && \frac{2}{N} \\ \vdots && && && && \vdots \\ \frac{2}{N} && \frac{2}{N} && \dots && \dots && (\frac{2}{N}-1) \end{bmatrix} \end{matrix}

这个矩阵作用于任意向量会起到什么效果呢？假设我们有个向量\(\sum_{k=0}^{N-1}\alpha_k|k\rangle\)，把这个矩阵作用于它：

\begin{matrix} \begin{bmatrix} \frac{2}{N}-1 && \frac{2}{N} && \frac{2}{N} && \dots && \frac{2}{N} \\ \frac{2}{N} && \frac{2}{N}-1 && \frac{2}{N} && \dots && \frac{2}{N} \\ \vdots && && && && \vdots \\ \frac{2}{N} && \frac{2}{N} && \dots && \dots && \frac{2}{N}-1 \end{bmatrix} \begin{bmatrix} \alpha_0 \\ \alpha_1 \\ \vdots \\ \alpha_{N-1} \end{bmatrix} \\ = \begin{bmatrix} -\alpha_0+2\langle\alpha\rangle \\ -\alpha_1+2\langle\alpha\rangle \\ \vdots \\ -\alpha_{N-1}+2\langle\alpha\rangle \end{bmatrix} = \begin{bmatrix} -\alpha_0 \\ -\alpha_1 \\ \vdots \\ -\alpha_{N-1} \end{bmatrix} + \begin{bmatrix} 2\langle\alpha\rangle \\ 2\langle\alpha\rangle \\ \vdots \\ 2\langle\alpha\rangle \end{bmatrix} \end{matrix}

其中的\(\langle\alpha\rangle\)是所有分量\(\alpha_k\)的平均值：\(\langle\alpha\rangle=\frac{1}{N}\sum_{k=0}^{N-1}\alpha_k\)

上面这个式子，加号左边就是原向量乘-1，而加号右边的向量，所有分量都相同，都是\(2\langle\alpha\rangle\)，归一化后就是无差别叠加态\(|\psi\rangle\)。两者相加，得到的是什么？看下面的图就可以直观的理解了：

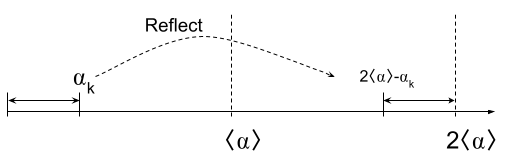
所以，\(2|\psi\rangle\langle\psi|-I\)作用在任意向量上，其实就是把输入向量对\(|\psi\rangle\)做 反射 ！

总结一下，G变换实际上就是连续两个反射操作：

• 首先对\(|\alpha\rangle\)轴做反射，即其中的Oracle变换
• 然后对\(|\psi\rangle\)做反射，即其中的\(2|\psi\rangle\langle\psi|-I\)

连续两步反射操作合在一起，其实就是把输入的向量进行了 旋转 。那么这个旋转角度是多少呢？我们在图里画一下就能明白了：

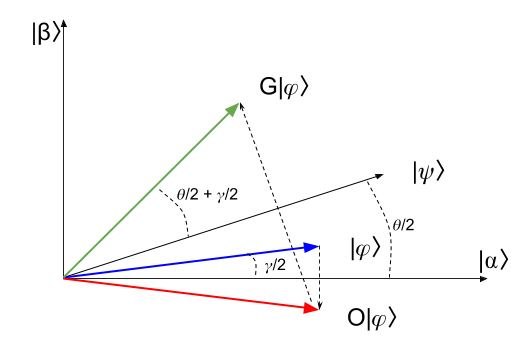
假设我们有个输入向量\(|\phi\rangle\)，它和\(|\alpha\rangle\)轴之间的夹角是\(\gamma/2\)。经过G变换的两次反射后，它和\(|\alpha\rangle\)轴的夹角变成了\(\theta/2+\theta/2+\gamma/2 = \theta+\gamma/2\)。也就是说，输入向量经过一次G变换后，朝着\(|\beta\rangle\)轴旋转了\(\theta\)。而\(|\beta\rangle\)轴意味着什么呢？它是所有 正确答案 的叠加态啊！如果系统的状态转到非常接近\(|\beta\rangle\)轴，测量就能得到正确答案！

所以， 我们每做一次G变换，就让系统的状态朝着\(|\beta\rangle\)轴旋转了\(\theta\) 。那么我们把这个过程重复多次，让系统非常接近\(|\beta\rangle\)轴，然后进行测量，就能以非常高的概率得到正确答案！

Grover算法需要试多少次能找到答案呢？这个问题实际上就是问，从初始状态\(|\psi\rangle\)出发，需要旋转多少次能接近\(|\beta\rangle\)轴？我们来做一个简要的分析。

前面分析过，G变换就是将系统状态朝\(|\beta\rangle\)旋转\(\theta\)。因此G可以写成这样的矩阵：

\begin{bmatrix} \cos\theta && -\sin\theta \\ \sin\theta && cos\theta \end{bmatrix}

• 一开始系统处于初始状态\(|\psi\rangle\)，和\(|\alpha\rangle\)轴的夹角是\(\theta/2\)。
• 每次G变换，将状态向量朝着\(|\beta\rangle\)旋转\(\theta\)。
• 经过k次G变换后，系统状态向量和\(|\alpha\rangle\)的夹角是\(\frac{2k+1}{2}\theta\)： \[ G^k|\psi\rangle = \cos(\frac{2k+1}{2}\theta)|\alpha\rangle + \sin(\frac{2k+1}{2}\theta)|\beta\rangle \]

我们的目标是尽可能接近\(|\beta\rangle\)轴，因此需要\(\sin(\frac{2k+1}{2}\theta)\)尽可能接近1，也就是\(\frac{2k+1}{2}\theta\)尽可能接近\(\pi/2\)。因此： \[ \frac{2k+1}{2}\theta \approx \frac{\pi}{2} \]

\[ k \approx (\frac{\pi}{2\theta} - \frac{1}{2}) \]

又因为k是整数，所以有\(k=round(\frac{\pi}{2\theta} - \frac{1}{2})\)。

我们知道 \[ \sin\frac{\theta}{2} = \sqrt{\frac{M}{N}} \]

同时假设搜索空间很大，N远大于M，我们可以做这样的近似： \[ \sin\frac{\theta}{2} \approx \frac{\theta}{2} \]

连起来我们就有这样的近似： \[ \frac{\theta}{2} \approx \sqrt{\frac{M}{N}} \]

把这个近似代入到前面k的式子里： \[ k=round(\frac{\pi}{2\theta} - \frac{1}{2}) \approx round(\frac{\pi}{4}\sqrt{\frac{N}{M}} - \frac{1}{2}) \]

可见需要旋转的次数k是\(O(\sqrt{\frac{N}{M}})\)。当M=1，也就是N个元素里只有1个正确答案的时候，k就是\(O(\sqrt{N})\)。所以，量子搜索算法相对于经典计算机，是\(O(N)\)到\(O(\sqrt{N})\)的加速。

想象一下，如果N个元素中有超过一半的正确答案，\(M>N/2\)，会发生什么？

在这种情况下，Grover算法的性能反而会变差！为什么呢？其实用刚才的几何图像想象一下就明白了，因为每次旋转的角度太多了，转过头了！

这种情况有两种解决办法：

1. 干脆不用量子搜索了，直接随机抽；
2. 把搜索空间扩大一倍，也就是N变成2N，这样正确答案不就少于一半了？实现方法也不难，给电路增加一个量子比特，规定如果它是\(|1\rangle\)，f(x)就返回0，否则就看其他的n位。这样就可以继续用Grover算法来搜索，这时旋转次数就变成了\(O(\sqrt{\frac{2N}{M}})\)，还是\(O(\sqrt{\frac{N}{M}})\)级别。