聊聊量子搜索算法(Grover算法) - 1
Ping Zhou, 2021-01-25
今天来聊一下量子计算里面的一个经典算法:量子搜索算法(Grover算法)。
搜索问题
假设我们有N个无结构的元素,比如很多指纹信息,我们的任务是从中找出符合某些要求的元素。为方便讨论,我们给这些元素编号,从0开始一直到N-1,并且其中只有1个符合我们要找的条件。如果我们用经典计算机来搜索的话,只能一个一个元素的试,看它是否符合要求,因此需要试的次数为\(O(N)\)。但是如果使用量子计算机,只需要试\(O(\sqrt{N})\)次数就可以找到。和经典计算机相比,虽然这不是指数级别的加速,但也相当可观了,尤其是如果“判断元素是否符合要求”这个操作很费力的话,减少判断次数的收益也会很大。
这个问题可以进一步抽象:我们有N个数(元素编号),这里为了方便讨论,假设\(N=2^{n}\),即编号可以用一个n位二进制数来表示。然后我们有一个判断函数f,给它输入编号x(n位二进制数),它判断该编号对应的元素是否符合要求,如果符合就返回1,否则返回0。
\[ f : \{0, 1\}^{n} \rightarrow \{0, 1\} \]
你可能会问:我都知道判断函数f了,为什么还需要查询呢?这里需要分清“找到符合条件的元素”和“判断元素是否符合条件”的区别。前者是“搜索”,而后者是“检验”。还是拿指纹做例子:警察在犯罪现场发现了嫌疑人的指纹,但是光有指纹并不能找到对应的嫌疑人,需要拿着指纹去和指纹库里的样本比对。这个“找到对应嫌疑人”的过程就是搜索,而“和指纹库里的样本进行比对”的过程就是检验,也就是前面说的判断函数f。
量子搜索算法(Grover算法)
定义了搜索问题,接下来讨论量子搜索算法。
量子搜索电路
量子搜索算法(Grover算法)是一个迭代的过程,主要思路是从初始状态出发,重复进行多次变换,让系统越来越接近目标状态,最后进行测量,就能以很高的概率得到正确结果。
量子搜索的电路图长这样:
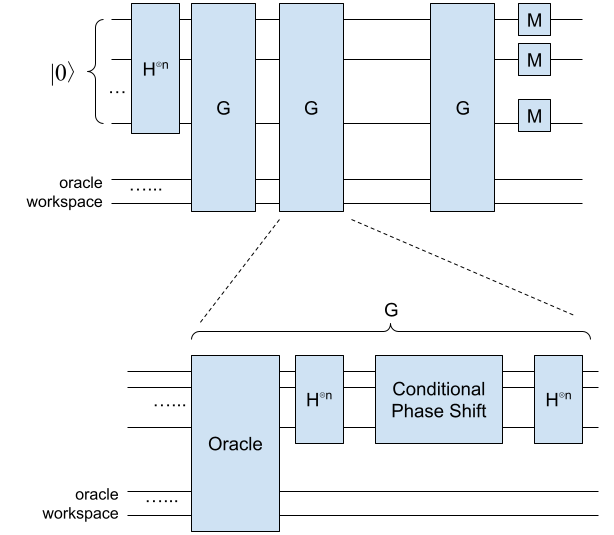
整个算法大致分成这样几步:
- 在输入端,我们需要准备一组量子比特,包括n个用来搜索的\(|0\rangle\),以及用于操作辅助量子比特的工作区(workspace)。这些辅助量子比特相当于程序里的临时变量,因此我们不用关心工作区的内部操作,只需要讨论前面的n个搜索用的量子比特。
- 计算的第一步,用H门把这n个量子比特从初始的\(|0\rangle\)变成无差别叠加态,也就是把\(|0\dots0\rangle\)变成\(\frac{1}{N}\sum_{x=0}^{N-1}|x\rangle\)(其中\(N=2^{n}\))。
- 然后,对这些量子比特进行G变换(后面会详细介绍),这个过程反复迭代多次。
- 最后在输出端测量,得到结果(n位二进制数)。
你可能会问,这个算法里的第3步里,需要多少次迭代(重复多少次G变换)呢?
答案是重复\(O(\sqrt{N})\)次后,我们就能以很高的概率得到正确结果。这个结果是怎么来的?后文分析原理的时候会详细讨论。现在先看看G变换里面是啥。
G变换
我们把量子搜索算法里每次迭代的过程称为G变换,这个G变换内部又分成4个步骤。
G变换的第一步:Oracle
首先要做什么?看过我之前文章的读者应该能猜到,要把判断函数f包装成量子计算机能用的可逆变换。套路和Deutsch问题类似,在输入的量子比特\(|x\rangle\)之外,增加一个辅助量子比特\(|y\rangle=\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)\),然后在输出端,原样输出\(|x\rangle\),外加输出\(|y \oplus f(x)\rangle\)。我们把这个变换称作Oracle,简称O变换:
\[ O|x\rangle|y\rangle = |x\rangle |y \oplus f(x)\rangle = |x\rangle \frac{1}{\sqrt{2}}(|0 \oplus f(x)\rangle - |1 \oplus f(x)\rangle) \]
(其中的\(\oplus\)表示异或)
我们知道判断函数f(x)的输出是0或者1,那么如果f(x)=1,上面右边就是\(|x\rangle \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)\),也就是\(|x\rangle |y\rangle\);而如果f(x)=1的话,上面右边就变成了\(|x\rangle \frac{1}{\sqrt{2}}(|1\rangle - |0\rangle)\),也就是\(-|x\rangle |y\rangle\)。这样一来,f(x)的输出就变成了相位:\(|x\rangle |y\rangle\)前面的正负号。所以Oracle变换可以写成:
\[ O|x\rangle|y\rangle = |x\rangle |y \oplus f(x)\rangle = (-1)^{f(x)} |x\rangle |y\rangle \]
如果我们忽略辅助量子比特\(|y\rangle=\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)\),只看前面的n个输入量子比特的话,Oracle的作用其实就是把输入的状态\(|x\rangle\)变成了 \((-1)^{f(x)} |x\rangle\)。 换句话说,Oracle把”f(x)是否为1“的答案标记成了输出的相位(+1/-1)。
G变换的第二步:n位H门
第二步,把刚才Oracle的输出,送入n位H门,\(H^{\otimes n}\)。
G变换的第三步:有条件的移相门
第三步是Conditional Phase Shift,它的作用很简单,就是对任何基态,如果它是\(|0\rangle\)就原样输出,否则就给它加上-1的相位。后面会详细分析这个门的含义。
G变换的第四步:n位H门
G变换的第四步,也是最后一步,是再做一次n位H门变换,即\(H^{\otimes n}\)。
接下来,我们来进一步分析G变换的各个步骤。
我们先来看第三步Conditional Phase Shift。它的作用是给输入的任何非\(|0\rangle\)基态加上一个-1的相位。所以这个Conditional Phase Shift变换可以写成这样的矩阵形式:
\begin{bmatrix} 1 && 0 && 0 && \dots && 0 \\ 0 && -1 && 0 && \dots && 0 \\ 0 && 0 && -1 && \dots && 0 \\ \vdots && && && \ddots && \vdots \\ 0 && 0 && 0 && \dots && -1 \\ \end{bmatrix}再简单推导一下,这个矩阵可以通过\(2|0\rangle \langle 0| - I\)得到:
\begin{matrix} |0\rangle \langle 0|= \begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \\ \end{bmatrix} \begin{bmatrix} 1 && 0 && \dots && 0 \end{bmatrix} \\ = \begin{bmatrix} 1 && 0 && \dots && 0 \\ 0 && 0 && \dots && 0 \\ \vdots && \vdots && \ddots && \\ 0 && 0 && \dots && 0 \\ \end{bmatrix} \end{matrix}因此有:
\begin{matrix} 2|0\rangle \langle 0| - I = \begin{bmatrix} 1 && 0 && \dots && 0 \\ 0 && -1 && \dots && 0 \\ \vdots && \vdots && \ddots && \\ 0 && 0 && \dots && -1 \\ \end{bmatrix} \end{matrix}所以,G变换的第三步Conditional Phase Shift可以写成\(2|0\rangle \langle 0| - I\)。
然后,我们再考察Conditional Phase Shift的两头,也就是第二步和第四步,分别都是n位H门。那么第二到第四步合在一起可以写成:
\[ H^{\otimes n}(2|0\rangle \langle 0| - I)H^{\otimes n} \]
简单推导可以知道,n位H门作用于\(|0\rangle\)得到的是无差别叠加态\(\frac{1}{N}\sum_{x=0}^{N-1}|x\rangle\),我们把它记作\(|\psi\rangle\),同时,\(HIH=I\),再运用分配率,把H放到括号里面去,上面的式子就变成了:
\[ 2|\psi \rangle \langle \psi | - I \]
也就是说,G变换的第二,三,四步合起来就是\(2|\psi \rangle \langle \psi | - I\)。
再加上第一步Oracle,整个G变换就可以写成:
\[ G=(2|\psi \rangle \langle \psi | - I)O \]
这个G变换重复多次,最后在输出端测量,就能以很高的概率得到正确答案。就是这么简单!
讨论到这里,我们知道了量子搜索算法的实现,但是为什么它能找到正确答案呢?在下文中我们将分析一下它的工作原理。