My previous article discussed Deutsch Problem in its simplest form - determine attribute of an unknown 1-bit function. Now what if we extend the function to having 2-bit input?

\[ f(x_0, x_1) \to \{0, 1\} \]

For 2-bit functions, there are 4 possible inputs: 00, 01, 10, 11. Outputs of the function are still 1-bit. So the truth table of the function will be like this:

input	output
00	0 or 1
01	0 or 1
10	0 or 1
11	0 or 1

We define the attribute of the function in a similar way as 1-bit Deutsh Problem. If the function returns a constant value regardless of the input, we call it constant. Apparently there are 2 constant functions (always return 0, or always return 1).

Balanced functions are a little bit tricky. How many balanced functions are there? From the table above we can see that in order for the function to be balanced, it must have exactly two 0s and two 1s in the “output” column. How many possible functions are there? Simple combination math tells us that there are 6 possible functions that meet this criteria. So there are 6 possible balanced functions out there.

Together, there are 8 possible 2-bit functions that are either constant or balanced. So the Two-Bit Deutsch Problem is like this: Someone randomly draws a function from these 8 candidates and gives it to us, and we need to determine whether it is constant or balanced.

Again, this function must be wrapped into a reversible operator \(U_f\) for us to evaluate it in quantum circuit. So we’ll ask the same thing to the person who gives us the function:

Instead of giving me function \(f(x_0, x_1)\), can you give me the corresponding \(U_f\) (still as a blind box)?

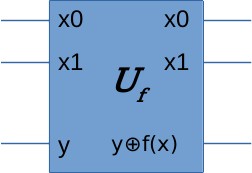
If we want to be 100% sure about the answer, how many evaluations do we need on a classical computer? Since there are 4 possible inputs, we need to evaluate more than half of all possible inputs. Evaluating 2 times won’t be enough (e.g. even we get 0 on the first two evaluations, the function may still be balanced). In general, if the input is n-bit, we’ll need \(2^{n-1}+1\) evaluations in order to be 100% sure about the function’s attribute. In other words, it grows exponentially as we expand the input.

On a quantum computer, on contrary, we’ll still only need to run the circuit once!

If you have read my prevoius note, you’ll notice that the quantum circuit for solving 2-Bit Deutsch Problem is very similar to the 1-bit version: It uses an auxilary qubit, puts H gates before and after the \(U_f\) block, then measures the two qubits.

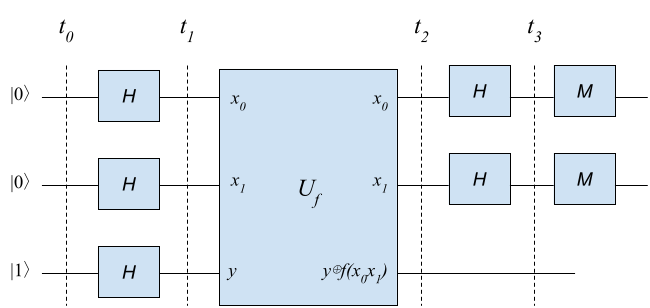
To save your time I’ll first put the conclusion here: We just need to run this circuit once and measure the first two qubits. If we get “00” from our measurement, the function must be constant. Otherwise it must be balanced.

To understand how it works, we do’ll do some time analysis on this circuit.

1. Time t0

Our system is at initial state \(|0\rangle|0\rangle|1\rangle\).

2. Time t1

All three qubits are in superposition. The first two are both at \(\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\), and the third one is at \(\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\). Since we use the first two qubits as the input of functon \(f(x_0x_1)\), we’ll consider their states together. The state of the two first qubits can be written as the tensor product (\(\otimes\)) of their states:

\[ \frac{1}{\sqrt{2}}(|0\rangle+|1\rangle) \otimes \frac{1}{\sqrt{2}}(|0\rangle+|1\rangle) = \frac{1}{2}(|00\rangle + |01\rangle + |10\rangle + |11\rangle) \]

Counting in the third qubit, the state of our system at time t1 can be written like this:

\[ \frac{1}{2}(|00\rangle + |01\rangle + |10\rangle + |11\rangle) \frac{1}{\sqrt{2}}(|0\rangle-|1\rangle) \]

3. Time t2

After \(U_f\), the first two qubits remain unchanged, but the third qubit becomes \(\frac{1}{\sqrt{2}}(|0 \oplus f(x_0x_1)\rangle-|1 \oplus f(x_0x_1)\rangle)\). Using the same Phase Kickback trick as last time, we examine the cases when \(f(x_0x_1)\) returns 0 and 1 respectively.

• If \(f(x_0x_1)\) is 0, then the third qubit becomes \(\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\).
• If \(f(x_0x_1)\) is 1, then the third qubit becomes \(\frac{1}{\sqrt{2}}(|1\rangle-|0\rangle)\). This is same as the previous case, except with a negative sign.

So the third qubit can be written as \((-1)^{f(x_0x_1)}\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\).

Adding back the first two qubits, the state of our system becomes: \[ \frac{1}{2}(|00\rangle + |01\rangle + |10\rangle + |11\rangle) \frac{1}{\sqrt{2}}(-1)^{f(x_0x_1)}(|0\rangle-|1\rangle) \]

And moving global phase to the front: \[ \frac{1}{2}(-1)^{f(x_0x_1)}(|00\rangle + |01\rangle + |10\rangle + |11\rangle) \frac{1}{\sqrt{2}}(|0\rangle-|1\rangle) \]

So the return value of function \(f(x_0x_1)\) becomes part of the global phase of our system state.

4. Time t3

We apply H gates to the first two qubits again. What will happen to the first two qubits (\(x_0\), \(x_1\))?

Before the two H gates (i.e. time t2), our system is at this state: \[ \frac{1}{2}(-1)^{f(x_0x_1)}(|00\rangle + |01\rangle + |10\rangle + |11\rangle) \frac{1}{\sqrt{2}}(|0\rangle-|1\rangle) \]

We don’t care about the third qubit any more, so we’ll just omit the third qubit in following discussion to keep our equations short. Before entering the two H gates, our first two qubits are in a superposition of these 4 states:

• \((-1)^{f(00)}|00\rangle\)
• \((-1)^{f(01)}|01\rangle\)
• \((-1)^{f(10)}|10\rangle\)
• \((-1)^{f(11)}|11\rangle\)

We’ll examine the four cases one by one.

• If our system is at state \((-1)^{f(00)}|00\rangle\) before entering the H gates, then applying H gates to the first two qubits gives us this (omitting the third qubit): \[ (-1)^{f(00)} H|0\rangle \otimes H|0\rangle \to (-1)^{f(00)} \frac{1}{\sqrt{2}}(|0\rangle+|1\rangle) \otimes \frac{1}{\sqrt{2}}(|0\rangle+|1\rangle) \] Which can be expanded into (we name it \(|\phi_{00}\rangle\) for convenience): \[|\phi_{00}\rangle = \frac{1}{2}(-1)^{f(00)} (|00\rangle+|10\rangle+|01\rangle+|11\rangle) \]
• Similary if our system is at \((-1)^{f(01)}|01\rangle\) at t2, we’ll get this state after applying the H gates (omitting the third qubit): \[|\phi_{01}\rangle = \frac{1}{2}(-1)^{f(01)} (|00\rangle+|10\rangle-|01\rangle-|11\rangle) \]
• If our system is at \((-1)^{f(10)}|10\rangle\) at t2, we’ll get this state after applying the H gates (omitting the third qubit): \[|\phi_{10}\rangle = \frac{1}{2}(-1)^{f(10)} (|00\rangle-|10\rangle + |01\rangle-|11\rangle) \]
• If our system is at \((-1)^{f(01)}|01\rangle\) at t2, we’ll get this state after applying the H gates (omitting the third qubit): \[|\phi_{11}\rangle = \frac{1}{2}(-1)^{f(11)} (|00\rangle-|10\rangle-|01\rangle+|11\rangle) \]

So at time t3, our system will be in a superposition of the 4 states above (\(|\phi_{00}\rangle\), \(|\phi_{01}\rangle\), \(|\phi_{10}\rangle\), \(|\phi_{11}\rangle\)), with equal amplitudes. Regrouping all the items according to the 4 base states (\(|00\rangle\), \(|01\rangle\), \(|10\rangle\), \(|11\rangle\)) and we’ll get something this:

\begin{matrix} \frac{1}{2} [(-1)^{f(00)} + (-1)^{f(01)} + (-1)^{f(10)} + (-1)^{f(11)}]|00\rangle + \\ \frac{1}{2} [(-1)^{f(00)} - (-1)^{f(01)} + (-1)^{f(10)} - (-1)^{f(11)}]|01\rangle + \\ \frac{1}{2} [(-1)^{f(00)} + (-1)^{f(01)} - (-1)^{f(10)} - (-1)^{f(11)}]|10\rangle + \\ \frac{1}{2} [(-1)^{f(00)} - (-1)^{f(01)} - (-1)^{f(10)} + (-1)^{f(11)}]|11\rangle \end{matrix}

What does this tell us? It tells us that our system is in a superposition of the 4 base states (\(|00\rangle\), \(|01\rangle\), \(|10\rangle\), \(|11\rangle\)), and the bracket in front of each base state (the \(\frac{1}{2}[\dots \dots]\) stuff) is the amplitude of each base state. If we measure the first two qubits at this moment, we’ll get one of the 4 results (00, 01, 10, 11) with probabilities determined by their respective amplitudes.

Do you see where we are going now?

If \(f(x_0x_1)\) is a constant function, then the four terms \((-1)^{f(00)}\), \((-1)^{f(01)}\), \((-1)^{f(10)}\), \((-1)^{f(11)}\) will be all the same (either 1 or -1). Among the four brackets above, only the one on \(|00\rangle\) will be non-zero. All other three brackets will be zero. If we measure the first two qubits, we should always get “00”.

If \(f(x_0x_1)\) is balanced, we should see two 1s and two -1s among the four terms \((-1)^{f(00)}\), \((-1)^{f(01)}\), \((-1)^{f(10)}\), \((-1)^{f(11)}\). It is easy to verify that the bracket on \(|00\rangle\) will always be zero. In other words it has zero amplitude. If we measure the first two qubits at this moment, we should never get “00”.

This is how our quantum circuit solves the 2-bit Deutsh Problem - we run the circuit once and measure the first two qubits, and we’ll able to tell if the function is constant or balanced.

In this article, we see how we could extend Deutsch Problem to 2-bits and solve it with quantum computing. When we expand the size of input, number of evaluations will grow exponentially on a classical computer (if we want to be 100% sure about the attribute of the function). But with quantum computing, we still only need to run the circuit once to get the answer.