量子算法之Simon问题
Ping Zhou, 2021-07-07
随手翻到一个Simon问题,今天就来聊聊它。Simon问题和之前讨论的Deutsch问题有点类似,也是一个用量子计算机能够达到指数级加速的问题。
什么是Simon问题?
和Deutsch问题类似,假设有人给我们一个函数f(x),内部实现未知,只知道它输入n位二进制数,输出也是n位二进制数。用数学语言描述就是这样:
\begin{matrix} f: \{ 0,1 \}^n \rightarrow \{ 0,1 \}^n \end{matrix}然后又知道存在某个数a,使得 \(f(y)=f(x)\) 当且仅当 \(y=x \oplus a\) ,这个a也称作函数f(x)的周期。为方便讨论,假设a不是0。
Simon问题要解决的,就是求解这个周期a的值。
在经典计算机上,这是一个困难的问题。因为f(x)是未知的,我们能做的就是从0到 \(2^n-1\) 中,每次选一个数作为输入计算f(x),直到发现重复的输出。最坏情况下,需要遍历超过一半的输入,即 \(2^{n-1}+1\) 次。根据Birthday Paradox,这个问题在经典计算机上需要的查询次数(时间复杂度)是 \(O(2^{n/2})\) 。
而在量子计算机上,我们只需要运行电路 \(O(n)\) 次就能以任意高的成功率得到结果。相对经典计算机,这是 指数级别 的加速!
Simon问题的量子算法
和之前的其他量子算法一样,首先我们得把函数f(x)包装成可逆变换 \(U_f\) :

然后放到Simon问题的量子电路里:
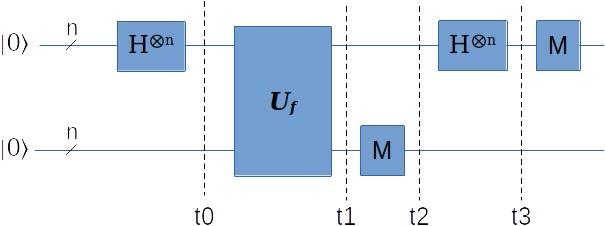
接下来我们来详细分析一下这个量子算法的过程。
t0时刻
第一个寄存器经过n位的H变换,变成 \(|0\rangle\) 到 \(|2^n-1\rangle\) 的叠加态,即 \(\frac{1}{2^{n/2}}\sum_{x=0}^{2^n-1}|x\rangle\) 。
第二个寄存器状态是 \(|0\rangle\) 。
所以合起来,t0时刻的状态是 \(\frac{1}{2^{n/2}}\sum_{x=0}^{2^n-1}|x\rangle|0\rangle\)
t1时刻
经过 \(U_f\) 变换,两个寄存器进入纠缠态,第一个寄存器还是 \(\frac{1}{2^{n/2}}\sum_{x=0}^{2^n-1}|x\rangle\) ,第二个寄存器变成了 \(|f(x)\rangle\) 。所以系统状态是:
\(\frac{1}{2^{n/2}}\sum_{x=0}^{2^n-1}|x\rangle|f(x)\rangle\)
t2时刻
对第二个寄存器进行测量,使它坍缩到某个值 \(z=f(x_0)\) 。
因为两个寄存器之前处于纠缠态,那么这时候第一个寄存器处于所有使得 \(f(x)=z\) 的 \(|x\rangle\) 的叠加态。根据函数的性质,只有 \(x_0, x_0 \oplus a\) 这两个输入能够让 \(f(x)\) 的输出是z。所以第一个寄存器的状态必然是这两个基态的叠加:
\(\frac{1}{\sqrt{2}} (|x_0\rangle + |x_0 \oplus a\rangle)\)
t3时刻
对第一个寄存器再作H变换。这里要讨论一下n位H变换的意义。
我们知道,单量子位的H变换有这样的性质:
\begin{matrix} H|0\rangle = \frac{1}{\sqrt 2} (|0\rangle + |1\rangle) \\ H|1\rangle = \frac{1}{\sqrt 2} (|0\rangle - |1\rangle) \\ \end{matrix}合起来可以写作这样的形式:
\begin{matrix} H|x\rangle = \frac{1}{\sqrt 2}\left( |0\rangle + (-1)^{x}|1\rangle \right) \\ = \frac{1}{\sqrt 2} \left( \sum_{y=0}^1 (-1)^{xy} \right) \end{matrix}所以n位H变换,也就是对n个量子位分别作H变换,整体状态可以写成这样:
\begin{matrix} H^{\otimes n}|x\rangle = \prod_{i=1}^n \left[ \frac{1}{\sqrt 2} \sum_{y_i=0}^1 (-1)^{x_i y_i} |y_i\rangle \right] \end{matrix}其中x, y都是n位二进制数:
\begin{matrix} x=x_1 x_2 \dots x_n \\ y=y_1 y_2 \dots y_n \end{matrix}上面这个式子的乘积展开后,可以进一步变成:
\begin{matrix} H^{\otimes n}|x\rangle = \frac{1}{2^{n/2}} \sum_{y=0}^{2^n-1} (-1)^{x \cdot y} |y\rangle \end{matrix}其中 \(x \cdot y = x_1y_1 \oplus x_2y_2 \oplus \dots \oplus x_ny_n\) ,就是x和y两个二进制数,逐位相乘再异或。这个结果可以用推理法来证明(即假设n位成立,证明n+1位也成立),具体推导这里就不写了,不然篇幅太长。
上面这个n位H变换的性质很重要,很多电路里都会用到。
回到Simon问题。在t3时刻,我们对第一个寄存器作H变换,而第一个寄存器在H变换前的状态是
\(\frac{1}{\sqrt{2}} (|x_0\rangle + |x_0 \oplus a\rangle)\)
也就是 \(|x_0\rangle\) 和 \(|x_0 \oplus a\rangle\) 的叠加。把它放到n位H变换里:
\begin{matrix} H^{\otimes n} \frac{1}{\sqrt{2}} (|x_0\rangle + |x_0 \oplus a\rangle) = \\ \frac{1}{2^{n/2}} \sum_{y=0}^{2^n-1} \left[ \frac{1}{\sqrt 2} \left( (-1)^{x_0 \cdot y} + (-1)^{(x_0 \oplus a) \cdot y} |y\rangle \right) \right] = \\ \frac{1}{2^{(n+1)/2}} \sum_{y=0}^{2^n-1} \left[ (-1)^{x_0 \cdot y} + (-1)^{(x_0 \oplus a)\cdot y}\right] \end{matrix}然后我们看求和项里的东西:
\begin{matrix} (-1)^{x_0 \cdot y} + (-1)^{(x_0 \oplus a)\cdot y} = \\ (-1)^{x_0 \cdot y} + (-1)^{x_0 \cdot y \oplus a \cdot y} \end{matrix}\(a \cdot y\) 是“逐位相乘再异或”,结果只可能是0或1,我们分情况来讨论。
如果 \(a \cdot y = 1\) ,那么上面这个求和项就变成了:
\begin{matrix} (-1)^{x_0 \cdot y} + (-1)^{x_0 \cdot y \oplus 1} = 0 \end{matrix}这两个指数,右边那个比左边那个多了个 \(\oplus 1\) (与1异或),所以两个指数必然是0/1相反的,放到-1的指数上,必然一个是1,另一个是-1,所以两者之和必然是0。
相反,如果 \(a\cdot y=0\) ,那么上面这个求和项,两个指数相等:
\begin{matrix} (-1)^{x_0 \cdot y} + (-1)^{x_0 \cdot y \oplus 0} = \\ (-1)^{x_0 \cdot y} + (-1)^{x_0 \cdot y} = 2 \times (-1)^{x_0 \cdot y} \end{matrix}所以在t3时刻,所有 \(a\cdot y \ne 0\) 的 \(|y\rangle\) ,其振幅都是0,剩下的都是使得 \(a \cdot y=0\) 的 \(|y\rangle\) 。因此t3时刻的状态,就是所有这样的 \(|y\rangle\) 的叠加态。这样的 \(|y\rangle\) 一共有多少个呢?简单的说,如果 \(a \ne 0\) ,那么使得 \(a \cdot y=0\) 的y有 \(2^{n-1}\) 个。那么t3时刻的状态可以写作:
\begin{matrix} \frac{1}{2^{(n-1)/2}} \sum_{a \cdot y = 0} (-1)^{x_0 \cdot y}|y\rangle \end{matrix}现在,我们对第一个寄存器进行测量,会得到什么?
我们会随机得到某个二进制数y,并且它满足 \(a \cdot y = 0\) 。重复运行这个电路多次,我们可以得到一组y值 \(y_1, y_2, \dots, y_n\) ,它们都满足 \(a \cdot y_i = 0\) 。那么这些y值和未知的变量a,就可以组成一个方程组:
\begin{matrix} \left\{ \begin{array}{l} a \cdot y_1 = 0 \\ a \cdot y_2 = 0 \\ \vdots \\ a \cdot y_n = 0 \end{array} \right. \end{matrix}如果我们有n个互相线性独立的y值,就可以从这个方程组解出a的值!
性能分析
我们需要重复运行这个量子电路的次数,取决于我们什么时候能得到需要的线性独立的y值。
简单估算一下概率:
- 第1次运行,得到 \(y_1\) ,我们需要它不为0(是0的话就没意义了),得到这样的y值概率是 \(1-\frac{1}{2^{n-1}}\) ;
- 第2次运行,得到 \(y_2\) ,我们需要它与 \(y_1\) 互相线性独立,得到这样的y值概率是 \(1-\frac{2}{2^{n-1}}\) ;
- 第3次运行,得到 \(y_3\) ,我们需要它与 \(y_1, y_2\) 互相线性独立,得到这样的y值概率是 \(1-\frac{4}{2^{n-1}}\) ,为什么这么算,详细的就不展开了 :-);
- 第4次运行,得到 \(y_4\) ,我们需要它与 \(y_1, y_2, y_3\) 互相线性独立,得到这样的y值概率是 \(1-\frac{8}{2^{n-1}}\) ;
- ……
- 第n-1次运行,以此类推,得到符合条件的y值的概率是 \(1-\frac{2^{n-2}}{2^{n-1}}\) 。
所以,运行n-1次,得到n-1个线性独立的y值,概率是
\begin{matrix} (1-\frac{1}{2}) (1-\frac{1}{4}) (1-\frac{1}{8}) \dots (1-\frac{1}{2^{n-1}}) \\ \gt \prod_{k=1}^{\infty}(1-\frac{1}{2^k}) \approx 0.29 \end{matrix}所以,连续运行n-1次电路,得到符合条件的一组y值的概率大于四分之一,换句话说,失败的概率小于3/4。那么如果我们重复运行电路4mn次,失败的概率小于 \((1-\frac{1}{4})^{4m} < e^{-m}\) 。
因此,我们重复运行电路 \(O(n)\) 次,就能以任意高的成功率得到符合条件的一组y值,从而求解出函数的周期a。
Simon算法就聊到这里,感谢阅读!