量子傅立叶变换是Shor算法的核心步骤之一。今天我们回到Shor算法，看看如何用量子傅立叶变换来求解Order Finding和函数周期问题。

用量子计算机求解Order Finding问题，实质上是要找到函数 \(f(x)=a^x \mod N\) 的周期。

Shor算法的第一步，是构造函数f(x)对应的可逆变换 \(U_f\) （这里的 \(|x\rangle, |y\rangle\) 都是多个量子位组成的寄存器）：

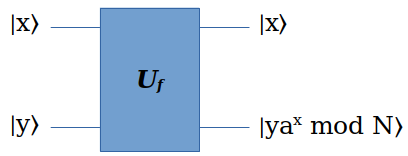
然后给它制备输入：

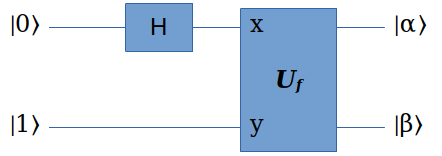
在输出端测量 \(|\beta\rangle\) ，使得它坍缩到某个值z，这时 \(\alpha\) 就会坍缩到 \(|l\rangle, |l+r\rangle, |l+2r\rangle, \dots, |l+Ar\rangle\) 的叠加态：

其中\(l\) 称为offset，是满足 \(a^l \mod N = z\) 的最小整数。假设 \(|\alpha\rangle\) 有n个量子位，那么A就是在0到 \(q=2^n\) 之间有多少个周期。

这里面， \(l, j\) 都是未知的，并且每次运行这个电路都有可能不同，不能直接从中导出周期r。所以下一步我们要做的，就是用量子傅立叶变换从中提取出有用的周期信息。

接着上一步：如果我们对 \(|\alpha\rangle\) 做量子傅立叶变换，会发生什么？

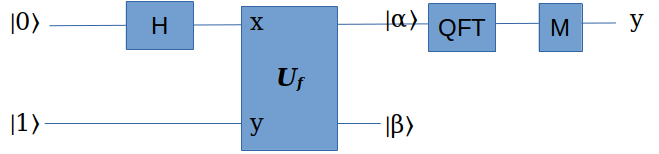
节省大家时间，先把答案放在这里，如果你有兴趣可以看我后文的推导。

如果我们对 \(|\alpha\rangle\) 做量子傅立叶变换，然后对它测量，得到某个值y，那么这个y值与 \(q=2^n\) 之间的比值，会非常接近某个整数k与周期r的比值。

好了，到了这一步，q是已知的（n个量子位， \(q=2^n\) ），y是测量得到的，也就是说左边这个分数是已知的。这个不等式告诉我们：测量得到的y，与q的比值，是 \(\frac{k}{r}\) 的一个 近似估计 。我们知道r小于N（N是要分解的数），所以右边是一个分母小于N的分数。如果我们能从左边 \(\frac{y}{q}\) 估计出一个和它很接近，并且分母小于N的分数，那这个分数的分母就有可能是我们要找的周期r！然后我们要做的就是对这个候选的r进行验证，如果它确实是函数f(x)的周期，那么问题解决，否则就重新运行Shor算法电路。

那么怎么从已知的 \(\frac{y}{q}\) 估计出右边的 \(\frac{k}{r}\) 呢？熟悉数论的朋友可能已经想到了—— 连分数算法 ！

举个栗子：我们的电路用了11个量子位，因此 \(q=2^n=2048\) ，量子傅立叶变换后测到y值是1537，于是 \(\frac{y}{q}=\frac{1537}{2048}\) 。用连分数算法可以得到一个近似的分数 \(\frac{3}{4}\) ，它的分母4就是可能的周期r。至于连分数算法，Python里有个fractions库可以直接用：

import fractions
r_candidate = fractions.Fraction.from_float(float(r/q)).limit_denominator(N)

就这样，我们用量子电路解决了Order Finding问题，再把结果放到Shor算法的整体流程里，因式分解问题也就解决了！

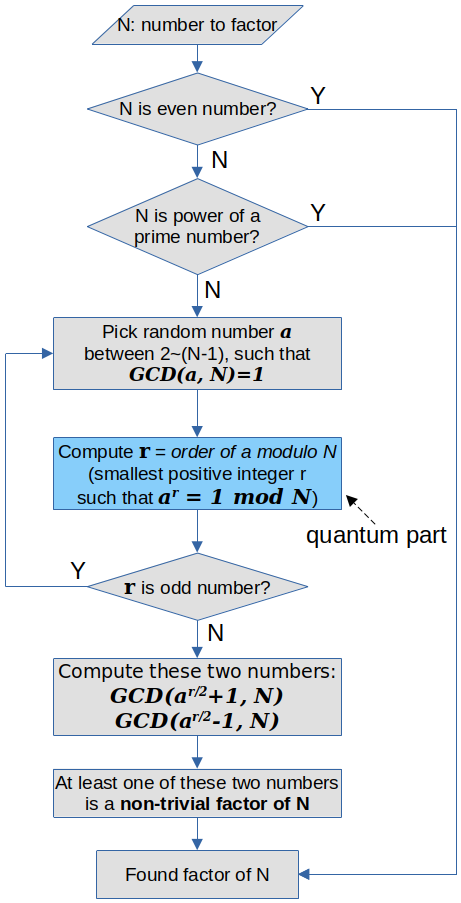
感谢阅读！