在前文『(5.2) Shor算法详解』中，我留了一个尾巴需要补充证明，今天就来填上这个坑，把补丁补上。

在前文讨论概率的推导过程中，有一步看起来不起眼，就是我们需要保证 \(\alpha\) 在0到 \(\pi/2\) 之间（其中 \(\alpha = \frac{A+1}{2} |\theta|\) ）。

但这一步其实很重要，为什么呢？因为只有保证 \(\alpha\) 在0到 \(\pi/2\) 之间，我们才能说 \(\sin \alpha \ge 2\alpha / \pi\) ：

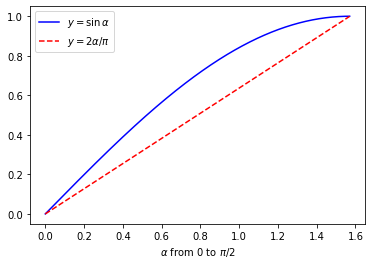
如果 \(\alpha\) 超过了 \(\pi/2\) ，这个性质就不成立了。而这个不等式，是后面我们推导出 \(|\tilde f(y)|^2\) ，也就是Shor算法成功概率的前提。

回顾一下， \(\theta = 2\pi \frac{ry \mod q}{q}\) ，并且y满足不等式 \(|ry \mod q| \le r/2\) 。

我们想要的不等式是：

怎样才能证明这个不等式呢？

我自己研究了一下，应该可以这样证明。

首先来看一下A是怎么计算的。如果我们把 \(l, l+r, \dots, l+Ar\) 画在数轴上，大致是这样的：

所以A的意义是在0到q-1之间，去掉开头的offset和最后的余数t，中间能容纳A个完整的周期（A+1个数据点）。不难得出： \(A=\lfloor \frac{q-l-1}{r} \rfloor - 1\) 。

令 \(m=A+1\) ，即 \(m=\lfloor \frac{q-l-1}{r} \rfloor\) ，我们可以把 \(|\tilde f(y)|^2\) 改写成这样：

我们已知y满足这个条件 \(|ry-kq| \le \frac{r}{2}\) ，也就是说， \(ry\) 在某个 \(kq\) 的 \(\pm \frac{r}{2}\) 范围内：

因此可以推出：

显然这里面的p，就相当于前文中 \(\theta = 2\pi \frac{ry \mod q}{q}\) 里的 \(ry \mod q\) ，即 \(\theta = 2\pi \frac{p}{q}\) 。

代入到前面的分子里：

这里利用了正弦函数的性质： \(|\sin (n\pi+p)| = |\sin p|\) ，以及 \(\sin(-p) = -\sin p\)

然后我们来看 \(\frac{m|p|}{q}\) 这部分。根据前面的讨论我们知道：

两者乘起来：

所以：

而我们之前定义的 \(\alpha\) ：

总算把前面的坑给填上了！ :-)