RSA生成公钥和私钥的流程大致是这样：

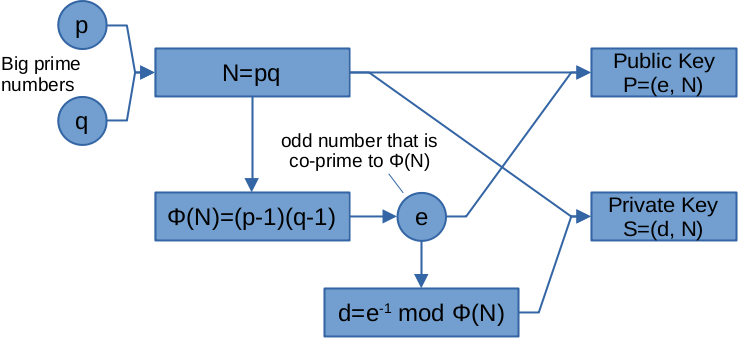
首先随机选两个很大的质数（p, q），然后用它们计算两个乘积：

• \(N=pq\)
• \(\phi(N)=(p-1)(q-1)\)

其中的 \(\phi(N)\) 也被称为『欧拉函数』，它的意思是“小于等于N并且与N互质的正整数的个数”。例如，如果某个数p是质数，那么显然有 \(\phi(p)=p-1\) 。为什么要用这个欧拉函数，后面会看到。

然后，随机选一个与 \(\phi(N)\) 互质的奇数e，计算它对于 \(\phi(N)\) 的『模逆』d，也就是找到某个正整数d，使得\(ed = 1 \mod \phi(N)\) ，这个数d可以用欧几里德算法高效计算出来。

最后，把e和N拼在一起，组成公钥P，而d和N拼在一起，组成私钥S。

有了公钥和私钥后，可以用公钥加密，然后用对应的私钥解密（下图左边是加密过程，右边是解密过程）：

我们把要加密的消息看作是一个固定长度的二进制数M，加密的时候，我们用公钥里的e和N，对M求e次幂，然后对N取模，得到加密后的消息E(M)：

\[ M^e \mod N \to E(M) \]

解密的方式和加密类似，但使用的是私钥里的d和N，对收到的消息E(M)求d次幂，然后对N取模，就能解密出原来的消息M。

\[ E(M)^d \mod N \to M \]

如果你对RSA算法的数学原理感兴趣，可以参阅本文最后的分析。

考虑M和N是否互质，分两种情况讨论。

1. M和N互质：

   假设我们拿到了加密后的信息E(M)，根据RSA的工作原理，解密的过程是对E(M)取d次幂：

   \[ E(M)^d \mod N = M^{ed} \mod N \]

   因为d是e对 \(\phi(N)\) 的模逆， \(ed = 1 \mod \phi(N)\) ，也就是说存在某个整数k，使得 \(ed = 1 + k\phi(N)\) 。把这个代入上面的公式，得到：

   \[ E(M)^d \mod N = M^{ed} \mod N = M^{1+k\phi(N)} \mod N = MM^{k\phi(N)} \mod N \]

   而根据欧拉函数的性质，有 \(M^{\phi(N)} = 1 \mod N\) ，因此对任意整数k，有 \(M^{k\phi(N)} = 1 \mod N\) ，代入上面的公式，解密后的消息就变成了：

   \[ E(M)^d \mod N = M^{ed} \mod N = MM^{k\phi(N)} \mod N = M \mod N \]

   解密成功，我们得到了原来的消息M。

2. M和N不互质：

   因为N是两个质数p和q的乘积，如果M和N不互质的话，p和q必有一个能整除M。假设p能整除M，即 \(M=0 \mod p\) ，因此 \(M^{ed} = 0 \mod p\) 。 接下来我们先假设q不能整除M （否则N也能整除M，这个特殊情况需要对M作预处理，后面再讨论），于是根据费马小定理有 \(M^{q-1}=1 \mod q\) 。 然后我们看到， \(M^{\phi(N)} = M^{(p-1)(q-1)}\) ，根据费马小定理已知 \(M^{q-1}=1 \mod q\) ，因此 \(M^{\phi(N)} = 1 \mod q\) 。 再用类似情况1中的推导（注意这里用的是模q）：

   \[ E(M)^d = M^{ed} = MM^{k\phi(N)} = M \mod q \]

   最后应用中国余数定理，可知：

   \[ E(M)^d = M^{ed} = M \mod (pq) = M \mod N \]

   p和q都整除M的特殊情况：这样的话N也能整除M， \(M=0 \mod N\) ，这样加密后的信息E(M)就变成了0，解密后也还是0。这种情况下，只需要对消息M作一些简单的预处理，例如加上一些padding，使得它不能被N整除即可。

假设p是质数，a是任意整数，则 1) \(a^{p} = a \mod p\) ；2) 并且如果a不能被p整除，则 \(a^{p-1} = 1 \mod p\) 。

证明：

先看一个引理：假设有质数p，任何小于p的正整数k，\({p \choose k}\) 必然能被p整除。为什么呢？其实很简单， \({p \choose k}=\frac{p!}{(p-k)!k!}\) ，因此下面的乘积可以写成：

\[ p(p-1)\dots(p-k+1)={p \choose k}k(k-1)\dots1 \]

然后因为k是正整数，上面这个公式左边必定能被p整除，而公式右边，因为k小于p， \(k(k-1)\dots1\) 这部分必定不能被p整除，这样一来， \({p \choose k}\) 必须能被p整除才能让左右两边相等。

接下来分别证明费马小定理及其推论。

1. 假设a是正整数（负整数的情况可类似推导），用推理法证明。 首先a=1的话，显然满足 \(a^{p} = a \mod p\) ；然后假设a满足条件 \(a^{p} = a \mod p\) ，考虑a+1的情况：

   \[ (a+1)^p = \sum_{k=0}^{p}{p \choose k}a^k \]

   注：参考二项式展开公式：

   \begin{matrix} (x+y)^n={n \choose 0}x^ny^0 + {n \choose 1}x^{n-1}y^1+\dots+{n \choose n-1}x^1y^{n-1}+{n \choose n}x^0y^n \\ =\sum^{n}_{k=0}{n \choose k}x^{n-k}y^k \end{matrix}

   根据前面的引理， \(\sum_{k=0}^{p}{p \choose k}a^k\) 这串东西里面，如果 \(1 \leq k \leq p-1\) ，那么 \({p \choose k}\) 必然能被p整除，对p取模后这些项都变成了0，只剩下两项分别是k=0和k=p：

   \[ (a+1)^p = \sum_{k=0}^{p}{p \choose k}a^k = {p \choose 0}a^0 + {p \choose p}a^p = (1+a^p) \mod p \]

   最后应用推理的假设 \(a^{p} = a \mod p\) ，可导出 \((a+1)^p=(a+1) \mod p\) ，证明完成。

2. 其实是 1) 的简单推论。如果a不能被p整除，那么a肯定有对p的模逆 \(a^{-1}\) ，于是： \[ a^{p-1} = a^{-1}a^p = a^{-1}a = 1 \mod p \]

欧拉函数 \(\phi(n)\) 的意思是“小于等于n并且与N互质的正整数的个数”。根据这个定义，任何质数p的欧拉函数显然就是p-1（从1到p-1都与p互质）。进一步，如果某个数n是质数p的a次幂，那么它的欧拉函数 \(\phi(p^a)\) 可以这样计算：

\[ \phi(p^a) = (p^a - 1) - (p^{a-1} - 1) = p^{a-1}(p-1) \]

这个公式怎么来的呢？我们知道 \(n=p^a\) 这个数，它的因子（除去它本身以外）其实就这些：

\[ p, 2p, 3p, \dots, (p^{a-1}-1)p \]

所以它一共有 \(p^{a-1}-1\) 个小于它本身的因子。那么从1到 \(p^a-1\) 这些数里面，去掉这 \(p^{a-1}-1\) 个 \(p^a\) 的因子，剩下的就都是和 \(p^a\) 互质的数。这些数总共有 \((p^a-1) - (p^{a-1}-1)\) 个，即 \(p^{a-1}(p-1)\) 个。

再进一步，如果两个数a和b互质，利用中国余数定理，我们还可以证明 \(\phi(ab) = \phi(a)\phi(b)\) 。

假设我们有一组两两互质的正整数 \(m_1, m_2, \dots, m_n\) ，另有一组 \(a_1, a_2, \dots, a_n\) ，列出这样一个方程组：

\begin{matrix} x = a_1 \mod m_1 \\ x = a_2 \mod m_2 \\ \dots \\ x = a_n \mod m_n \\ \end{matrix}

令 \(M=m_1m_2 \dots m_n\) ，这个方程组有解，并且任何两个解，都对模M相等。

证明：

我们用构造解的办法来证明。定义 \(M_i = M/m_i\) （也就是 \(M\) 缺了 \(m_i\) ），显然 \(m_i\) 和 \(M_i\) 是互质的，因此 \(M_i\) 对 \(m_i\) 存在模逆，我们记作 \(N_i\) 。然后我们定义 \(x = \sum_i a_iM_iN_i\) ，接下来证明这个x是上面方程组的解。

我们注意到， \(M_iN_i = 1 \mod m_i\) ，并且 \(M_iN_i = 0 \mod m_j\) (\(j \ne i\))。所以对x中的每一项 \(a_iM_iN_i\) ，只有对 \(m_i\) 取模的时候是 \(a_i\) ，对其他 \(m_j\) 取模都是0。

\begin{equation} a_iM_iN_i = \begin{cases} a_i \mod m_i & \\ 0 \mod m_j, & j \ne i \end{cases} \end{equation}

例如方程组的第一个方程 \(x = a_1 \mod m_1\) ，x对 \(m_1\) 取模，x所有相加的项中只有 \(a_1M_1N_1\) 这一项对 \(m_1\) 取模是\(a_1\) ，其他项都是0，所以x满足该方程 ，以此类推，可知x是该方程组的解。

然后再假设这个方程组有另一个解y，也满足方程组的所有方程，那么如果我们把它们相减：

\begin{matrix} x-y = (a_1 - a_1) = 0 \mod m_1 \\ x-y = (a_2 - a_2) = 0 \mod m_2 \\ \dots \\ x-y = (a_n - a_n) = 0 \mod m_n \\ \end{matrix}

就是说x-y可以被 \(m_1, m_2, \dots, m_n\) 每一个整除，再加上 \(m_1, m_2, \dots, m_n\) 两两互质，可知x-y必然能被 \(M=m_1m_2\dots m_n\) 整除，因此 \(y = x \mod M\) ，即y和x两个解对M取模相等。