前文说过，对于任意状态 \(|\psi\rangle\) ：

\begin{matrix} |\psi\rangle = \sum_{j=0}^{N-1}f(j)|j\rangle & (N=2^n) \end{matrix}

对它进行量子傅立叶变换QFT后，会得到一个新状态：

\begin{matrix} |\tilde\psi\rangle = QFT|\psi\rangle = \sum_{k=0}^{N-1}\tilde f(k)|k\rangle, \\\ \\\ \tilde f(k) = \frac{1}{\sqrt{N}} \sum_{j=0}^{N-1} e^{2\pi ijk/N} f(j) \\\ = \frac{1}{\sqrt{N}} \sum_{j=0}^{N-1} \omega^{jk} f(j) & (\omega=e^{2\pi i/N}) \\\ \end{matrix}

那么量子傅里叶逆变换 \(QFT^{-1}\) 是什么样的？

很简单，其实就是把e的指数加个负号：

\begin{matrix} |\phi\rangle = \sum_{k=0}^{N-1} \tilde f(k) |k\rangle \\\ \\\ QFT^{-1} |\phi\rangle = \sum_{j=0}^{N-1} g(j) |j\rangle \\\ \\\ g(j) = \frac{1}{\sqrt{N}} \sum_{k=0}^{N} \omega^{-jk} \tilde f(k) \\\ \end{matrix}

可以看到，量子傅立叶逆变换和QFT非常相似，唯一的区别就是e的指数上多了个负号。

为什么多个负号就变成逆变换了呢？下面我们来验证一下。

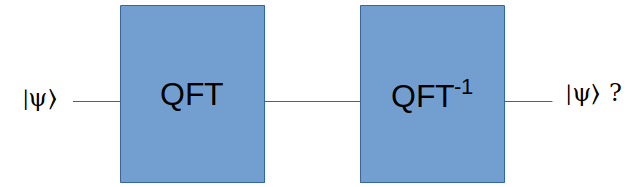
假如我们对一个状态 \(|\psi\rangle\) 作了QFT：

\begin{matrix} |\psi\rangle = \sum_{j=0}^{N-1}f(j)|j\rangle & (N=2^n)\\\ \\\ QFT|\psi\rangle = \sum_{k=0}^{N-1}\tilde f(k)|k\rangle \\\ \tilde f(k) = \frac{1}{\sqrt{N}} \sum_{m=0}^{N-1} e^{2\pi imk/N} f(m) \\\ = \frac{1}{\sqrt{N}} \sum_{m=0}^{N-1} \omega^{mk} f(m) & (\omega = e^{2\pi i/N}) \end{matrix}

那么对它作逆变换的话：

\begin{matrix} QFT^{-1} QFT|\psi\rangle = \sum_{j=0}^{N-1} g(j) |j\rangle \\\ \end{matrix}

所以我们验证的目标，是要证明 \(g(j) = f(j)\) ，也就是逆变换后回到最初的状态。

把 \(\tilde f(k)\) 代入到前面的公式里：

\begin{matrix} g(j) = \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} \omega^{-jk} \tilde f(k) \\\ = \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} \omega^{-jk} \left[ \frac{1}{\sqrt{N}} \sum_{m=0}^{N-1} \omega^{mk} f(m) \right] \\\ = \frac{1}{N} \sum_{k=0}^{N-1} \omega^{-jk} \sum_{m=0}^{N-1} \omega^{mk} f(m) \end{matrix}

这里面， \(j\) 是 \(g(j)\) 的参数，对每个 \(g(j)\) 来说是确定的，然后里面有2个嵌套的求和，分别遍历 \(k, m\) ，我们把两层求和项展开成二维的表就能看清楚：

	m=0	m=1	…	m=N-1
k=0	\(\omega^{0(0-j)}\)	\(\omega^{0(1-j)}\)	…	\(\omega^{0(N-1-j)}\)
k=1	\(\omega^{1(0-j)}\)	\(\omega^{1(1-j)}\)	…	\(\omega^{1(N-1-j)}\)
…	…	…	…	…
k=N-1	\(\omega^{(N-1)(0-j)}\)	\(\omega^{(N-1)(1-j)}\)	…	\(\omega^{(N-1)(N-1-j)}\)
	f(0)	f(1)	…	f(N-1)

这个二维表里面，每一列对应求和项里的一个 \(f(m)\) 的系数，而 \(g(j)\) 就是整个二维表之和。

然后分清况讨论：

如果某一列（例如第m列）有 \(m \ne j\) ，那么该列 \(f(m)\) 的系数就是：

\begin{matrix} \sum_{k=0}^{N-1} \omega^{k(m-j)} = \sum_{k=0}^{N-1} a^k && (a = \omega^{m-j} = e^{2\pi i(m-j)k/N}) \\\ \end{matrix}

根据几何级数性质， \(\sum_{k=0}^{N-1} a^k=\frac{a^N-1}{a-1}\) ，以及 \(a^N = e^{2\pi i(m-j)}=1\) ，可知：

\begin{matrix} \sum_{k=0}^{N-1} \omega^{k(m-j)} = \sum_{k=0}^{N-1} a^k = 0 \end{matrix}

所以当 \(m \ne j\) 的时候， \(f(m)\) 的系数是0。也就是说，这个二维表里面，除了第 \(j\) 列以外，其他的所有列系数之和都是0!

接下来看，如果 \(m=j\) ，也就是第 \(j\) 列的系数之和：

\begin{matrix} \sum_{k=0}^{N-1} \omega^{k(m-j)} = \sum_{k=0}^{N-1} \omega^0 = N \end{matrix}

综上所述， \(g(j)\) 的这个二维表里面，只有第 \(j\) 列，对应 \(f(j)\) 的系数加起来是非0，所以：

\begin{matrix} g(j) = \frac{1}{N} N f(j) = f(j) \end{matrix}

因此经过逆变换后又回到了最初的状态 \(|\psi\rangle=\sum_{k=0}^{N-1} f(j)|j\rangle\) ，我们验证了量子傅立叶逆变换的作用。