量子计算是现在的热门话题之一，很多人可能听说过诸如“量子霸权”之类的名词，那么量子计算为什么会被认为有可能比经典计算机更快呢？这里就从最简单的Deutsch问题入手，解析量子计算的一些基本思路，相信看完后你会对量子计算的潜力有更直观的认识。

首先要先解释一下后面讨论中用到的一些术语和基础知识。

量子比特（Qubit）

我们知道，一个经典比特（bit）只能表示两种状态（0或者1）。而一个量子比特除了 \(|0\rangle\) 和 \(|1\rangle\) 之外，还可以处于一种叫相干态（superposition）的状态，即“同时”处于 \(|0\rangle\) 和 \(|1\rangle\) 两种状态。这可以用 \(\alpha|0\rangle + \beta|1\rangle\) 来表示（ \(\alpha\) 和 \(\beta\) 都是复数）。一个常见的例子是 \(\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\) ，测量得到0和1的概率分别是50%。

量子计算电路里常见的几种门（变换）：

• I：Identity变换，简单说就是啥也不变，输入啥输出也是啥。
• H: Hadamard门，在这个例子里主要作用是制备相干态，因为H门可以把 \(|0\rangle\) 变成 \(\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\) ，而把 \(|1\rangle\) 变成 \(\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\) 。另外H变换还有个特性，就是HH=I，两个H变换互相抵消。
• Z：输入 \(|x\rangle\) ，输出 \((-1)^x|x\rangle\) ，例如输入 \(|0\rangle\) ，输出 \(|0\rangle\) ，而输入是 \(|1\rangle\) 的话，输出是 \(-|1\rangle\) 。
• X：简单说就是将输入取反，输入 \(|0\rangle\) 的话，输出 \(|1\rangle\) ，而输入 \(|1\rangle\) ，则输出 \(|0\rangle\) 。

另外，还有两个特性后面会用到：

\begin{matrix} HZH=X \\ HIH=I \end{matrix}

好了，需要了解的基础知识就这么些，接下来我们来看量子计算是如何加速Deutsch问题的。

假设我们有个函数f，输入和输出都是1个比特： \(y=f(x)\) ：

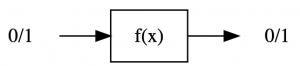
因为输入和输出都只有1个比特，这个函数无非就是这4种可能：

1. \(f(x)=0\) ，即不管x是0还是1，f(x)总是0，我们记作 \(f_0\)
2. \(f(x)=1\) ，即不管x是0还是1，f(x)总是1，我们记作 \(f_1\)
3. \(f(x)=x\) ，即f(x)输出比特和输入比特相同，我们记作 \(f_x\)
4. \(f(x) = \bar{x}\) ，即f(x)输出比特与输入比特相反，我们记作 \(f_\bar{x}\)

前两种可能，我们称为“常量”函数（constant），因为他们的输出是常量；而后两种我们称为“平衡”函数（balanced），因为他们所有可能的输出中间，0和1各占一半。

所谓的Deutsch问题，实际上是问：假如f(x)对我们而言是一个黑盒，也就是说我们不知道f(x)里面是怎么运作的，如何判断它是“常量”还是“平衡”的呢？

你也许会说，很简单啊，我们给f(x)喂一点输入，然后观察它的输出就行了啊，对不对？这个“喂输入，观察输出”的过程，我们称为对f(x)的 查询 。

那么下一个问题， 我们需要对f(x)做几次“查询”，才能知道它到底是“常量”还是“平衡”的呢？

稍微想一下就可以知道，1次查询是不够的。举个例子，我们给f(x)输入0，得到输出0，我们能够只根据这个结果判断f(x)的性质吗？显然不行！因为f(x)既有可能是常量（ \(f_0\) ），也有可能是平衡的（ \(f_x\) ），两者都能满足“输入0，输出0”。

所以，在经典世界里，我们需要对f(x)做2次查询，才能判断它是常量还是平衡。

那么有没有更快的办法，仅用1次查询就能判断出f(x)的性质呢？用量子计算可以做到！

在量子计算里，所有的变换都必须是**可逆**的，也就是“从输出能倒推出输入”。显然f(x)不一定能满足这个条件，所以首先要对它进行一下“包装处理”。

把原来的函数f(x)，包装一个成量子计算里的可逆变换 \(U_{f}\) ：

\(U_{f} |x\rangle |y\rangle = |x\rangle |y \oplus f(x)\rangle\)

这里的 \(|x\rangle\) ， \(|y\rangle\) 都是量子比特， \(\oplus\) 是“异或”运算符。包装后的 \(U_{f}\) ，输入两个量子比特 \(|x\rangle\) ， \(|y\rangle\) ，输出也是两个量子比特 \(|x\rangle\) ， \(|y \oplus f(x)\rangle\) ，如下图所示：

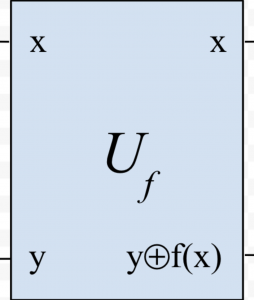
和原来的函数f(x)相比， \(U_{f}\) 多了一个“辅助输入”（ancillary），即 \(|y\rangle\) 。这个辅助输入的作用，很快我们就能看到。

前面说过，如果我们给H门一个 \(|1\rangle\) 输入，可以得到一个相干态（superposition）的量子比特：

\(H|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\)

这个状态通常又被记作 \(|-\rangle\)

有意思的事情来了，如果我们把这个状态 \(|-\rangle\) 作为辅助输入 \(|y\rangle\) 喂给 \(U_{f}\) ，会发生什么呢？

前面说过， \(U_{f} |x\rangle |y\rangle = |x\rangle |y \oplus f(x)\rangle\) ， 代入 \(|y\rangle=|-\rangle=\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\) ，我们可以得到：

\begin{matrix} U_{f}|x\rangle|y\rangle = \\ |x\rangle\frac{1}{\sqrt{2}}(|0\oplus f(x)-1\oplus f(x)\rangle) = \\ |x\rangle\frac{1}{\sqrt{2}}(|0\oplus f(x)\rangle-|1\oplus f(x)\rangle) \end{matrix}

（这里利用了异或运算的分配律）

f(x)无非是0或者1：

• 如果f(x)=0，那么上面的结果就变成 \(|x\rangle\frac{1}{\sqrt{2}}(|0\oplus0\rangle-|1\oplus 0\rangle) = |x\rangle\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\) ，也就是 \(|x\rangle|-\rangle\)
• 如果f(x)=1，那么上面的结果就变成 \(|x\rangle\frac{1}{\sqrt{2}}(|0\oplus1\rangle-|1\oplus 1\rangle) = |x\rangle\frac{1}{\sqrt{2}}(|1\rangle-|0\rangle)\) ，也就是 \(-|x\rangle|-\rangle\)

把上面两种情况综合起来， \(U_{f}|x\rangle|-\rangle=(-1)^{f(x)}|x\rangle|-\rangle\) 。

看到没有？原先f(x)是在 \(|y\rangle\) 里的，现在跑到了输出端的正负号上： \((-1)^{f(x)}\) ，这个输出端的正负号，又称为 全局相位 。也就是说，如果我们给 \(U_{f}\) 喂一个辅助输入 \(|-\rangle\) ，就可以把把f(x)挪到输出端的“全局相位”（global phase）上！这是量子计算里一种常用的方法，叫做“phase kickback”。

但是全局相位本身是测量不出来的，这有什么用呢？别急，我们还有个输入 \(|x\rangle\) 没用呢！

现在考虑f(x)的四种可能情况： \(U_{f}|x\rangle|-\rangle=(-1)^{f(x)}|x\rangle|-\rangle\)

• \(f_0\) ：即f(x)总是0，那么 \(U_{f}|x\rangle|-\rangle= |x\rangle|-\rangle\) ，对输入 \(|x\rangle\) 来说，相当于一个 \(I\) 变换
• \(f_1\) ：即f(x)总是1，那么 \(U_{f}|x\rangle|-\rangle= -|x\rangle|-\rangle\) ，对输入 \(|x\rangle\) 来说，相当于一个 \(-I\) 变换
• \(f_x\) ：即 \(f(x)=x\) ，那么 \(U_{f}|x\rangle|-\rangle= (-1)^x |x\rangle|-\rangle\) ，还记得前面说的 \(Z\) 变换吗？对输入 \(|x\rangle\) 来说，这相当于一个 \(Z\) 变换，即 \(U_{f}|x\rangle|-\rangle= Z|x\rangle|-\rangle\)
• \(f_{\bar{x}}\) ：即 \(f(x)=\bar{x}\) ，那么 \(U_{f}|x\rangle|-\rangle= (-1)^{-x} |x\rangle|-\rangle = -(-1)^{x} |x\rangle|-\rangle\) ，对输入 \(|x\rangle\) 来说，这相当于一个 \(-Z\) 变换，即 \(U_{f}|x\rangle|-\rangle= -Z|x\rangle|-\rangle\)

再综合一下，经过 \(U_{f}|x\rangle|-\rangle\) 后， \(f_0\) 和 \(f_1\) （“常量”函数）分别变成了 \(I\) 和 \(-I\) ，而 \(f_x\) 和 \(f_{\bar{x}}\) （“平衡”函数）则分别变成了 \(Z\) 和 \(-Z\) ！这正是我们想要区分的！

但是问题又来了：如何区分 \(I\) 和 \(Z\) 呢？ \(Z\) 变换只改变相位，而正负相位经过测量后是区分不出来的，怎么办呢？

还记得前面提到的这两个公式吗？

\begin{matrix} HZH=X \\ HIH=I \end{matrix}

如果我们在 \(U_{f}|x\rangle|-\rangle\) 的两边，各放上一个H门，那么 \(f_0\) 和 \(f_1\) （“常量”函数）就会变成 \(\pm I\) ，而 \(f_x\) 和 \(f_{\bar{x}}\) （“平衡”函数）则会变成 \(\pm X\) 。 \(X\) 变换是干啥的？就是把 \(|0\rangle\) 变成 \(|1\rangle\) ，把 \(|1\rangle\) 变成 \(|0\rangle\) 啊！

到这一步，我们给 \(|x\rangle\) 输入 \(|0\rangle\) ，在输出端进行测量，会得到什么结果？

如果f(x)是“常量”函数（ \(f_0\) 或 \(f_1\) ），那么对 \(|x\rangle\) 就是一个 \(\pm I\) 变换，在输出端测量，得到的仍然是 \(|0\rangle\) ；

如果f(x)是“平衡”函数（ \(f_x\) 或 \(f_{\bar{x}}\) ），那么对 \(|x\rangle\) 就是一个 \(\pm X\) 变换，在输出端测量，我们会得到 \(|1\rangle\) ！

最后我们得到的量子计算电路是这样的：

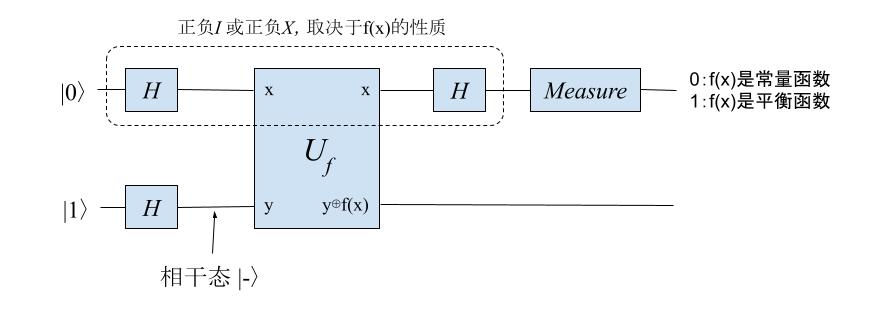
更重要的是，整个过程我们只对电路进行了 一次测量 ，也就是说， 对f(x)进行了一次“查询” ，我们就能知道f(x)是“常量”还是“平衡”的，而在经典计算机里，这个性质需要2次查询才能知道！

为什么会有这样的加速呢？我认为最关键的是通过输入相干态的 \(|y\rangle\) ，在 \(U_{f}\) 内部实际上实现了对所有可能状态的并行查询！

不要小看这里1次和2次的差别，这实质上体现了量子计算相对于经典计算的并行性，理论上可能会带来指数级的加速！

当然，Deutsch问题本身没有太多实用价值，但它显示了在某些场景下量子计算机可以比经典计算机更快。理解Deutsch算法可以帮助我们更好的理解量子计算的内在并行性。至于有潜力实用化的量子计算算法，例如Grover搜索，Shor因式分解等，以后有空再说。