量子机器学习:TensorFlow Quantum入门
Ping Zhou, 2020-11-27
注:转载请注明作者,本文也发布在作者的个人公众号上。
相关代码请见作者的Github。
TensorFlow Quantum
TensorFlow Quantum (TFQ) 是谷歌在2020年发布的 量子机器学习框架 ,它能够帮助开发者方便的创建经典+量子结合的混合机器学习模型。量子+机器学习,两个热门的名词结合在一起,听上去很酷!但是你可能会问,这个框架是如何把经典和量子世界结合起来的呢?所谓的”经典-量子混合模型“又是如何工作的?在这个笔记里,我会结合谷歌的“Hello, many world”示例,实际讲解一下在TFQ下量子机器学习模型的搭建和工作原理。
基本概念
要理解TFQ的代码,首先需要了解一些量子计算的基本概念。
量子比特和状态向量
你可能在很多地方已经听到过量子比特(Qubit)的概念。一个经典比特在任意时刻只能处于两个状态中的一个,而量子比特则可以处于两个状态的叠加态:
\(|\psi\rangle = \alpha|0\rangle + \beta|1\rangle\)
其中, \(\alpha\) 和 \(\beta\) 都是复数,并且 \(|\alpha|^2+|\beta|^2=1\) 。如果我们对这个量子比特进行测量,得到两个状态的概率分别是 \(|\alpha|^2\) 和 \(|\beta|^2\) 。
因此,一个量子比特的状态可以用一个**状态向量**来表示:
\begin{matrix} \begin{pmatrix} \alpha \\ \beta \end{pmatrix} \end{matrix}如果我们的系统里有多个量子比特,每个量子比特有相应的状态向量,那么这个系统的状态向量就是这些量子比特的**张量积**(tensor product)。例如一个系统有两个量子比特 \(\begin{pmatrix}\alpha_1 \\ \beta_1\end{pmatrix}\) 和 \(\begin{pmatrix}\alpha_2 \\ \beta_2\end{pmatrix}\) ,那么这个系统的状态向量就是:
\(\begin{pmatrix}\alpha_1 \\ \beta_1\end{pmatrix} \otimes \begin{pmatrix}\alpha_2 \\ \beta_2\end{pmatrix} = \begin{pmatrix} \alpha_1\alpha_2 \\ \alpha_1\beta_2 \\ \beta_1\alpha_2 \\ \beta_1\beta_2 \end{pmatrix}\)
在谷歌的量子计算框架[Cirq]里,模拟器运行的结果里有一个 final_state 成员,这就是系统的状态向量。详细信息请参见我的[另一篇笔记]。
量子比特另外一种重要的表示方法是 Bloch球 (Bloch Sphere)。每一个量子比特都可以表示为Bloch球面上的一个向量:

算符(Operators)和可观测量(Observables)
算符(Operators)
简单来说,算符就是把量子比特从一个状态变成另一个状态的变换。前面说到量子比特可以用向量来表示,因此算符实际上就是用来操作向量的矩阵。
可观测量(Observables)
什么是可观测量呢?简单说就是可测量的物理量,例如位置、动量等都可以算作可观测量。
在量子世界里,每个可观测量都对应一个叫做“厄米子”(Hermitian Operator)的算符,这类算符有一些特别的属性(例如它们和自身的共轭转置相等)。在这次的笔记里,我们使用的**Z算符**就是其中之一,其矩阵表示长这样:
\(Z= \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\)
期望值
前面说到,状态向量描述了一个系统的当前状态。如果我们知道了这个向量,我们就掌握的系统的所有状态信息。 但是,状态向量实际上只有在使用模拟器的时候才能看到。在真实的环境中,我们能得到的是系统的**期望值**。
期望值是来自概率论的一个概念,它的意思是所有可能结果和它们各自概率的加权之和。例如我们掷骰子,每次能得到1~6之间的一个数,假设得到每个数的概率相同,都是1/6,那么掷骰子的期望值就是:
\(\frac{1}{6}\times 1 + \frac{1}{6}\times 2 + ... + \frac{1}{6}\times 6 = 3.5\)
在量子世界里,如果我们要谈期望值,除了当前状态外,我们还需要说明是在**哪个算符(可观测量)上的期望值**。
为什么呢?因为使用不同的可观测量,相应的期望值也会不同!这就像同一个向量投影到不同的轴上,得到的值是不一样的!
在这个笔记里,我们使用的是Z算符,所以谈到期望值,我们说的其实是“当前状态在Z算符上的期望值”。
接下来的问题是: 如何计算当前状态在Z算符上的期望值呢?
详细的推导过程这里就不列出了,不过你可能已经猜到了,这个值就是状态向量在Z轴上的投影,也就是 \(\cos\theta\) 。
我们可以看几个例子来验证上面的结论:

- 如果当前状态是在Bloch球的北极,那么测量结果100%肯定是+Z,期望值是 \(\cos 0 = 1\) 。
- 如果当前状态是在Bloch球的南极,那么测量结果100%肯定是-Z,期望值是 \(\cos\pi = -1\) 。
- 如果当前状态在上面图中Bloch球的D点,测量结果50%可能是+Z,50%可能是-Z,期望值是 \(\cos\frac{\pi}{2}=0\) 。
问题描述
要理解我们的量子机器学习模型,首先我们得搞明白它要解决的是什么问题。
假设我们想要运行一个量子电路,那么在运行前我们先得准备初始的量子比特作为输入(通常是一组 \(|0\rangle\) 或 \(|1\rangle\) )。
在模拟器里,这些初始量子比特都是完美的 \(|0\rangle\) 或 \(|1\rangle\) ,但是在现实环境里,我们的电路会有各种噪声干扰,导致这些量子比特偏离我们想要的状态。如果我们从Bloch球来理解,这些噪声实际上相当于把原来“完美”的量子比特在X,Y,Z轴上作了旋转,使其偏离了原有的状态。这个噪声干扰的过程可以用下面的电路来表示:

\(\beta_1\) , \(\beta_2\) , \(\beta_3\) 参数是噪声产生的旋转角度,对我们来说是未知的。
显然,如果不对这些量子比特进行**校准**(Calibrate)就输入给量子电路用,就不能得到我们想要的结果。怎么进行校准呢?很简单,我们给它再加上一组X,Y,Z旋转,把它转回到我们要的目标状态!

而校准所需的角度参数 \(\theta_1\) , \(\theta_2\) , \(\theta_3\) ,就是我们的量子机器学习模型所要解决的问题。
量子机器学习模型
原版的例子直接跳入大量细节,可能不太容易理解,在这里我从全局角度出发,应该会更容易明白。我们要搭建的,是一个用来校准量子比特噪声的机器学习模型:

那么作为机器学习模型,我们要回答这几个问题:
- 模型的输入(dataset)是什么?
- 模型的训练标签(labels)是什么?
- 模型的输出是什么?
我把整个过程画了这样一张图,然后结合这张图分别解释其中的各个部分,相信能更好的帮助你理解:

输入数据集(Datasets)
输入的数据集(Dataset)包含两个部分:命令(commands)和噪声电路(noisy circuit)。
Commands
Commands是我们希望量子比特达到的目标状态的代号。例如,“Command 0“表示我们想要的到一个处于Bloch球的北极(+Z)的量子比特,而“Command 1”表示我们想要一个处于南极(-Z)的量子比特。
Noisy input
这部分就是模拟噪声的电路。TFQ里提供了一个 tfq.convert_to_tensor 函数来把电路转换成TensorFlow能看懂的tensor:
circuit_tensor = tfq.convert_to_tensor([circuit])
训练标签(Labels)
这里的训练标签,就是 我们想要量子比特达到的目标状态的期望值 :
当输入Command 0时,我们想要量子比特的期望值是1;而输入Command 1时,我们想要量子比特的期望值是-1。
因此,训练标签(对应Command 0,1)的内容就是 [1, -1] 。
模型输出
模型的输出,就是量子比特校准后的期望值。
经典-量子混合模型
我们这个模型里有经典和量子两部分。
- 经典部分 就是图中的Controller,就是一个普通的深度神经网络。它的输出是校准角度 \(\theta_1\) , \(\theta_2\) , \(\theta_3\) 。
- 量子部分 是图中的“ControllPQC”层(我们给它取名“expectationlayer“)。它从Controller那里拿到校准角度参数 \(\theta_1\) , \(\theta_2\) , \(\theta_3\) ,用它们运行校准电路(“modelcircuit”),然后把输出(校准后的期望值)反馈给Controller进行训练。
总结起来,我们想让这个模型干的事就是:
给你一个被噪声干扰的量子比特(circuitinput)和两个命令(Command 0, 1),要求在输入Command 0的时候输出一个期望值是1的量子比特,而在输入Command 1的时候输出期望值是-1的量子比特。
这样捋一遍是不是就清楚了?:-)
代码解析
安装TFQ
TensorFlow Quantum依赖TensorFlow 2.3.1+,最简单的方法是通过pip:
pip install -q tensorflow==2.3.1
pip install -q tensorflow-quantum
导入依赖包
import tensorflow as tf import tensorflow_quantum as tfq import cirq import sympy import numpy as np # visualization tools %matplotlib inline import matplotlib.pyplot as plt from cirq.contrib.svg import SVGCircuit
准备输入数据
首先创建一个量子比特对象:
# This creates a "perfect" qubit at |0>. # It will be fed into the noisy preparation circuit to emulate a noisy qubit. qubit = cirq.GridQubit(0, 0)
创建输入数据集 - Command 0,1:
# Dataset: commands_input (0 and 1) commands = np.array([[0], [1]], dtype=np.float32)
创建噪声电路。这里我们随机产生一组角度,作为X/Y/Z轴旋转的参数。创建好的Circuit对象,需要转换成TensorFlow的tensor。
另外要注意的是,这里需要2个噪声电路的副本,分别对应前面Command数组的两项。
# Dataset: circuit_input (noisy preparation) # This emulates the noisy qubit by applying X/Y/Z rotations with random angles. random_rotations = np.random.uniform(0, 2 * np.pi, 3) noisy_preparation = cirq.Circuit( cirq.rx(random_rotations[0])(qubit), cirq.ry(random_rotations[1])(qubit), cirq.rz(random_rotations[2])(qubit) ) # Convert the circuit object to tensor. # Two copies of the circuit because we have two commands (0 and 1) to train. datapoint_circuits = tfq.convert_to_tensor([ noisy_preparation ] * 2)
打印出来看看,可以看到原先“完美”的量子比特(Cirq里默认初始状态是 \(|0\rangle\) )被随机在X,Y,Z轴上做了旋转。
# Print out the noisy qubit print(random_rotations) print(noisy_preparation)
[3.84902356 3.3647054 3.03737137] (0, 0): ───Rx(1.23π)───Ry(1.07π)───Rz(0.967π)───
创建Keras输入端,分别对应Commands和noisypreparation。
# Create keras inputs from the datasets circuits_input = tf.keras.Input(shape=(), # The circuit-tensor has dtype `tf.string` dtype=tf.string, name='circuits_input') commands_input = tf.keras.Input(shape=(1,), dtype=tf.dtypes.float32, name='commands_input')
准备训练标签
训练标签就是目标状态的期望值,也就是1和-1(分别对应输入Command 0和1)。
# Labels: target expecation values (1 for command 0, -1 for command 1) expected_outputs = np.array([[1], [-1]], dtype=np.float32)
搭建量子机器学习模型
经典部分就是一个普通的深度神经网络(DNN)。因为这里只有一个量子比特,一个简单的2层DNN就够了。
# Classical part of our model - "controller". # Since the problem is fairly small, a simple DNN is enough. controller = tf.keras.Sequential([ tf.keras.layers.Dense(10, activation='elu'), tf.keras.layers.Dense(3) ])
然后是量子部分。首先我们用Cirq API搭建校准电路( model_circuit ),带3个参数 \(\theta_1\) , \(\theta_2\) , \(\theta_3\) :
# Quantum part of our model - "model_circuit" # Parameters that the classical NN will feed values into. control_params = sympy.symbols('theta_1 theta_2 theta_3') # Create the parameterized circuit. qubit = cirq.GridQubit(0, 0) model_circuit = cirq.Circuit( cirq.rz(control_params[0])(qubit), cirq.ry(control_params[1])(qubit), cirq.rx(control_params[2])(qubit)) SVGCircuit(model_circuit)

要把这个电路接到模型里去,我们需要把它包装成一个Keras layer。
这里我们用的是Parameterized Quantum Circuit“ (PQC): tfq.layers.ControlledPQC 。我们给它取名 expectation_layer ,因为它的输出是期望值。
你可能注意到我们在创建PQC层的时候用到了 operators 参数。前面说过,谈期望值必须说明是在哪个算符上,这里通过 operators 参数,我们告诉PQC用Z算符来计算期望值。
PQC创建完成,接下来我们就可以把它同噪声电路( circuits_input )和校准参数(controller的输出 dense_2 )接起来了。
dense_2 = controller(commands_input) # TFQ layer for classically controlled circuits. expectation_layer = tfq.layers.ControlledPQC(model_circuit, # Observe Z operators = cirq.Z(qubit)) expectation = expectation_layer([circuits_input, dense_2])
创建模型:
model = tf.keras.Model(inputs=[circuits_input, commands_input], outputs=expectation)
这个模型可视化出来是这样的,感觉还是我前面画的那个更清楚:
tf.keras.utils.plot_model(model, show_shapes=True, dpi=70)
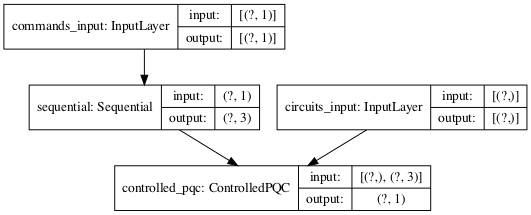
模型训练
训练过程就和普通的DNN差不多,这里用Adam优化器和MSE损失函数。
# Now we can train the model... optimizer = tf.keras.optimizers.Adam(learning_rate=0.05) loss = tf.keras.losses.MeanSquaredError() model.compile(optimizer=optimizer, loss=loss) history = model.fit(x=[datapoint_circuits, commands], y=expected_outputs, epochs=30, verbose=0)
把训练过程可视化出来:
# Plot the history - looks good! plt.plot(history.history['loss']) plt.title("Learning to Control a Qubit") plt.xlabel("Iterations") plt.ylabel("Error in Control") plt.show()
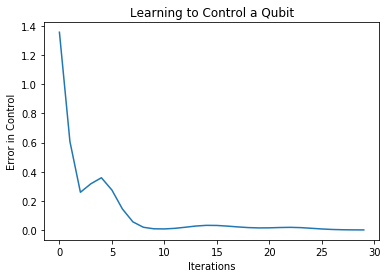
验证
模型训练好了,我们给它输入Command 0和1,看看它输出的期望值:
model([datapoint_circuits, commands])
<tf.Tensor: shape=(2, 1), dtype=float32, numpy=
array([[ 0.9891974],
[-0.9958328]], dtype=float32)>
可以看到,输出的期望值非常接近我们的目标。可见我们的模型把被噪声干扰的量子比特校准回了需要的状态,我们的第一个量子机器学习模型就成功完成了!
拓展
这个例子还可以进一步扩展跟通用的情况,使用其他的算符。下次有空再说。
感谢阅读!