所谓“遇事不决，量子力学”，“量子纠缠”是量子力学中的一个重要现象，也是科幻故事中经常用到的填坑大杀器。实际上，量子纠缠是真实的物理现象，也是实现量子通信的核心之一。今天我们就来聊聊量子纠缠是怎么回事。

假设我们有2个量子比特A和B，初始状态都是\(|0\rangle\)，然后搭一个简单的电路：

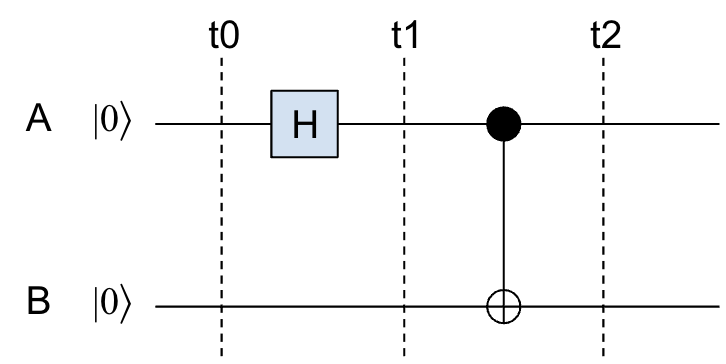
只需要一个H门和一个CNOT门，就能让A和B之间形成量子纠缠！

不信？我们来分析一下。

t0时刻，两个量子比特都是 \(|0\rangle\) ，整个系统的状态是 \(|00\rangle\) 。

t1时刻，A经过H门后变成了相干态 \(\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\) ，而B不变还是 \(|0\rangle\) ，整个系统状态变成 \(\frac{1}{\sqrt{2}}(|00\rangle + |10\rangle)\) 。

t2时刻，经过一个CNOT门。CNOT意思是“Controlled NOT”，就是说当A是1的话，B就取反，否则B不变。因为这里A已经是相干态（ \(|0\rangle\) 和 \(|1\rangle\) 的叠加），那么经过这个CNOT门以后，A如果是 \(|0\rangle\) ，那么B不变还是 \(|0\rangle\) ，而A如果是 \(|1\rangle\) ，那么B就从 \(|0\rangle\) 变成 \(|1\rangle\) 。所以整个系统经过这个CNOT门后，就变成了这样一个状态：

\(\frac{1}{\sqrt{2}}(|00\rangle + |11\rangle)\)

看出什么没有？在这个状态下，A和B要么都是 \(|0\rangle\) ，要么都是 \(|1\rangle\) ！也就是说，如果我们测量A得到0，那么我们知道B测量得到肯定也是0，反之如果我们测量A得到1，那么B肯定也是1。通过这个电路，我们把A和B两个量子比特的状态“纠缠”在了一起，这个状态就叫做“ 纠缠态 ”。

这时候，如果我们把A和B分开，A和B之间还会处于纠缠态吗？答案是肯定的，只要它们没有退相干，A和B仍然处于会量子纠缠状态。即使我们把B送到银河系的另一端，它们仍然会“纠缠”在一起。甚至，如果我们对其中之一做进一步的量子变换，只要不导致退相干，它们之间仍然会保持纠缠态！

这就是量子纠缠的原理，是不是挺简单的？:-)

常见误解：量子纠缠能实现超光速通信？

信息的传递不可能超光速，否则会导致因果律的崩溃。表面上看，一端的测量会导致另一端的状态坍缩，这个作用是“瞬时”的，但是实际上这个动作没有在两端之间传递任何信息，因为测量得到0和1完全是随机的。