量子计算编程实战 – 双比特Deutsch问题
Ping Zhou, 2020-09-04
在上一篇 “一文看懂量子计算机的威力 – 从Deutsch问题说起” 中,我们看到了量子计算机只需一次查询就可以判断函数的特性。但是在那个例子中,我们讨论的是一个简单的单比特函数,如果把输入扩展到多比特,量子计算机是否仍然只需要一次查询呢?今天我们就结合谷歌的Cirq框架,看看量子计算的 指数级 加速。
双比特Deutsch问题
首先和上次一样,假设我们有个函数f,但这次函数f输入2个比特,输出1个比特。这个函数f对我们是黑盒,我们不知道这个函数内部是怎么运作的,只能通过喂给它不同的输入,观察输出。因为输入有2个比特,因此共有4种可能的输入00,01,10,11。
- 如果f无论什么输入,输出始终是0或者1,我们称它为“常量”函数,记作 \(f_0\) 或者 \(f_1\) ;
- 如果f的输出,0和1各占一半,我们称它为“平衡”函数。平衡函数有多少种可能呢?这个问题就相当于说,我们在下面表中的4个输出位置,需要填两个0和两个1,有几种填法?用简单的排列组合可以知道,一共有6种,也就是说一共有6个“平衡”函数。
| 输入 | 输出 |
| --- | --- |
| 00 | 0或者1 |
| 01 | 0或者1 |
| 10 | 0或者1 |
| 11 | 0或者1 |
- 当然,函数f也有可能既不是常量,也不是平衡的,例如上面的表里面,输出栏里可以填上三个0。
双比特Deutsch问题是问,假如我们已经知道函数f要么是常量,要么是平衡的,如何判断它是常量还是平衡的呢?
对于n比特输入,经典计算机需要至少查询一半可能的输入,也就是 \(2^{n-1}+1\) 次(在这个例子里n=2,所以需要查询3次)。显然随着输入比特数的增加,计算复杂性(需要查询的次数)是指数上升的。而 如果用量子计算机,无论输入n有多大,我们始终只需要对函数f进行一次查询!
怎么做到呢?套路和上次一样,引入一个辅助输入y,把函数f包装成量子比特版本Uf:
\begin{matrix} U_f |x_0\rangle |x_1\rangle |y\rangle \to |x_0\rangle |x_1\rangle |y \oplus f(x_0x_1)\rangle \end{matrix}然后在两边加上Hadamard门,电路也和上次的单比特电路差不多:
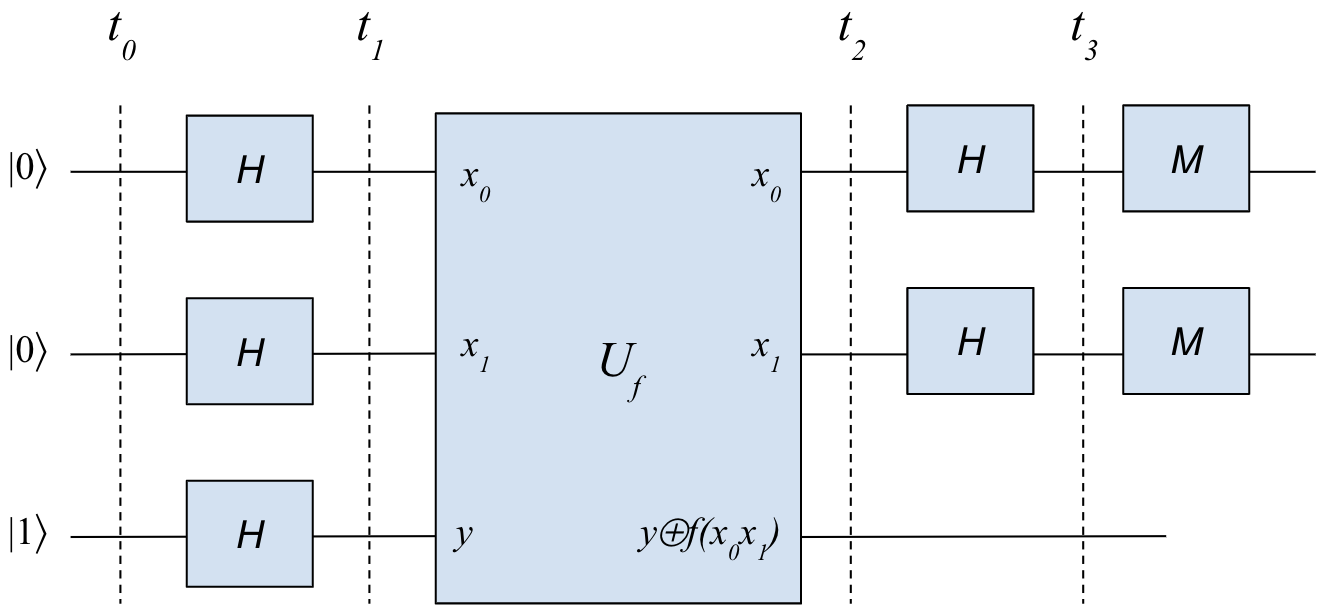
猜猜看在输出端测量,我们会得到啥?
这里先把结论放在这里 :如果输出端得到的是全0,那么函数f一定是常量函数,反之它就是平衡函数。
原理解析
下面我们做一些推导,可以帮助您理解其中的原理。如果您不感兴趣,可以直接跳到下一篇的实战部分。其实推导并不难,不要被公式吓到 :-)
为便于分析,我在前面的电路图中标出了时间(t0, t1, t2, t3)。
在 时间t0 ,电路的状态是 \(|0\rangle|0\rangle|1\rangle\) 。
在 时间t1 ,前两个量子比特都处于 \(\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)\) 状态,第三个处于 \(\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\) 状态。如果我们把前两个量子比特放一起考虑,相当于把他们的状态做一个卷积,也就是:
\begin{matrix} \frac{1}{\sqrt{2}}(|0\rangle+|1\rangle) \otimes \frac{1}{\sqrt{2}}(|0\rangle+|1\rangle) = \frac{1}{2}(|00\rangle + |01\rangle + |10\rangle + |11\rangle) \end{matrix}加上第三个辅助量子比特,整个电路的状态就是
\begin{matrix} \frac{1}{2}(|00\rangle + |01\rangle + |10\rangle + |11\rangle) \frac{1}{\sqrt{2}}(|0\rangle-|1\rangle) \end{matrix}在 时间t2 ,经过了Uf后,前两个量子比特不变,第三个量子比特变成了 \(\frac{1}{\sqrt{2}}(|f(x_0x_1)\rangle-|1 \oplus f(x_0x_1)\rangle)\) 。然后和上次一样的套路: \(f(x_0x_1)\) 如果是0,那么第三个量子比特就是 \(\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)\) ,反之就是 \(\frac{1}{\sqrt{2}}(|1\rangle-|0\rangle)\) 。所以第三个量子比特这时的状态可以写成 \(\frac{1}{\sqrt{2}}(-1)^{f(x_0x_1)}(|0\rangle-|1\rangle)\) 。这就是我们喜闻乐见的phase kickback套路,把函数f踢到相位上去了。整个状态这时候变成:
\begin{matrix} \frac{1}{2}(|00\rangle + |01\rangle + |10\rangle + |11\rangle) \frac{1}{\sqrt{2}}(-1)^{f(x_0x_1)}(|0\rangle-|1\rangle)$ \end{matrix}这里面的相位 \((-1)^{f(x_0x_1)}\) 是全局的,可以放到前面去,变成:
\begin{matrix} \frac{1}{2}(-1)^{f(x_0x_1)}(|00\rangle + |01\rangle + |10\rangle + |11\rangle) \frac{1}{\sqrt{2}}(|0\rangle-|1\rangle) \end{matrix}这时候,如果我们扔掉辅助量子比特,只看前两个量子比特,我们看到是:
\begin{matrix} \frac{1}{2}((-1)^{f(00)}|00\rangle + (-1)^{f(01)}|01\rangle + (-1)^{f(10)}|10\rangle + (-1)^{f(11)}|11\rangle) \end{matrix}这里是2比特的情况,如果是更多的n比特,写成更通用的就是
\begin{matrix} \frac{1}{\sqrt{2^n}}\sum_{x=0}^{2^n-1}(-1)^{f(x)}|x\rangle \end{matrix}接下来 时间t3 ,再次经过H门,前两个量子比特的状态如何变化呢?这里以2比特为例做一下直观的分析,在进入两个H门之前的状态,实际上是下面四种状态的叠加:
- \((-1)^{f(00)}|00\rangle\)
- \((-1)^{f(01)}|01\rangle\)
- \((-1)^{f(10)}|10\rangle\)
- \((-1)^{f(11)}|11\rangle\)
我们可以分别对这四个状态进行分析:
- \((-1)^{f(00)}|00\rangle\) :经过H门变成 $(-1)f(00)
H|0⟩ ⊗ H|0⟩ → (-1)f(00) \frac{1}{\sqrt{2}}(|0⟩+|1⟩) ⊗ \frac{1}{\sqrt{2}}(|0⟩+|1⟩)$ ,进一步展开成 \(\frac{1}{2}(-1)^{f(00)} (|00\rangle+|10\rangle+|01\rangle+|11\rangle)\)
- \((-1)^{f(01)}|01\rangle\) :同样的,经过H门展开成 $\frac{1}{2}(-1)f(00)
(|00⟩+|10⟩-|01⟩-|11⟩)$
- \((-1)^{f(10)}|10\rangle\) :经过H门展开成 $\frac{1}{2}(-1)f(00)
(|00⟩-|10⟩ + |01⟩-|11⟩)$
- \((-1)^{f(11)}|11\rangle\) :经过H门展开成 $\frac{1}{2}(-1)f(00)
(|00⟩-|10⟩-|01⟩+|11⟩)$
上面这四个状态叠加起来,再按照 \(|00\rangle\) , \(|01\rangle\) , \(|10\rangle\) , \(|11\rangle\) 分组,变成这样:
\begin{matrix} \frac{1}{2} [(-1)^{f(00)} + (-1)^{f(01)} + (-1)^{f(10)} + (-1)^{f(11)}]|00\rangle + \\ \frac{1}{2} [(-1)^{f(00)} - (-1)^{f(01)} + (-1)^{f(10)} - (-1)^{f(11)}]|01\rangle + \\ \frac{1}{2} [(-1)^{f(00)} + (-1)^{f(01)} - (-1)^{f(10)} - (-1)^{f(11)}]|10\rangle + \\ \frac{1}{2} [(-1)^{f(00)} - (-1)^{f(01)} - (-1)^{f(10)} + (-1)^{f(11)}]|11\rangle \end{matrix}如果我们在这时测量这两个量子比特,会得到00,01,10,11四个结果之一。而上面四个方括号里的东西,就是这四个状态各自的强度,也就是测量得到这四个结果各自的概率。例如测量得到00的概率是 \(\frac{1}{2} [(-1)^{f(00)} + (-1)^{f(01)} + (-1)^{f(10)} + (-1)^{f(11)}]\) 。
到这里,是不是看出点什么名堂了?我们来看函数f的性质:
- 如果f是常量函数,那么 \((-1)^{f(00)}\) , \((-1)^{f(01)}\) , \((-1)^{f(10)}\) , \((-1)^{f(11)}\) 这四个全是1或者全是-1,上面四个中括号里面,只有第一个会是非零(四个数相加得到4或者-4),其他三个中括号里都是两个正两个负,互相抵消为零。也就是说,如果f是常量,那么除了 \(|00\rangle\) 外,其他状态的强度都是零。我们在这时进行测量,得到的结果一定是00!
- 如果f是平衡函数,那么 \((-1)^{f(00)}\) , \((-1)^{f(01)}\) , \((-1)^{f(10)}\) , \((-1)^{f(11)}\) 这四个中,两个是1,两个是-1。放到上面的四个方括号里,第一个方括号必然是零(四个数相加,其中两个1,两个-1),所以 \(|00\rangle\) 的强度是零,而后面三个方括号必有一个非零。所以我们在这时进行测量,得到的结果一定是01,10,11其中之一,而不可能是00!
所以结论是,我们在输出端测量前两个量子比特,如果结果是00,那么函数f是常量,如果不是,那么函数f是平衡的。更重要的是,虽然输入变成了2个比特,我们仍然只需要对函数f做一次查询,而且这个方法可以进一步扩展到n个比特,都只需要一次查询。可见,随着输入规模的扩大,经典计算机的计算复杂度上升,量子计算机的优势会越来越明显。
在下一篇“实战篇”里,我会结合谷歌的Cirq量子计算编程框架,演示双比特Deutsch问题的模拟实现。