If you are familiar with the recent frenzy about ChatGPT, Bard and other large language models, you probably already know about Transformer, the key building block behind these models.

The key algorithm inside Transformer block is Self Attention, which is commonly described as the following equation:

(NOTE: the scaling part in the softmax is omitted for brevity.)

Sometimes this equation is also written in an iterative way like this:

The above equation gives the “attention” vector at position t of the sequence. On the first glance, it seems pretty straightforward to map from the first equation to the second, given the definition of softmax:

But wait… how about the \(v_i\) in the 2nd equation?

To understanding the Self Attention mechanism deeper, I find it useful by looking into a bit more details into the math, especially how the first equation is mapped to the 2nd one.

Let’s start with the basics.

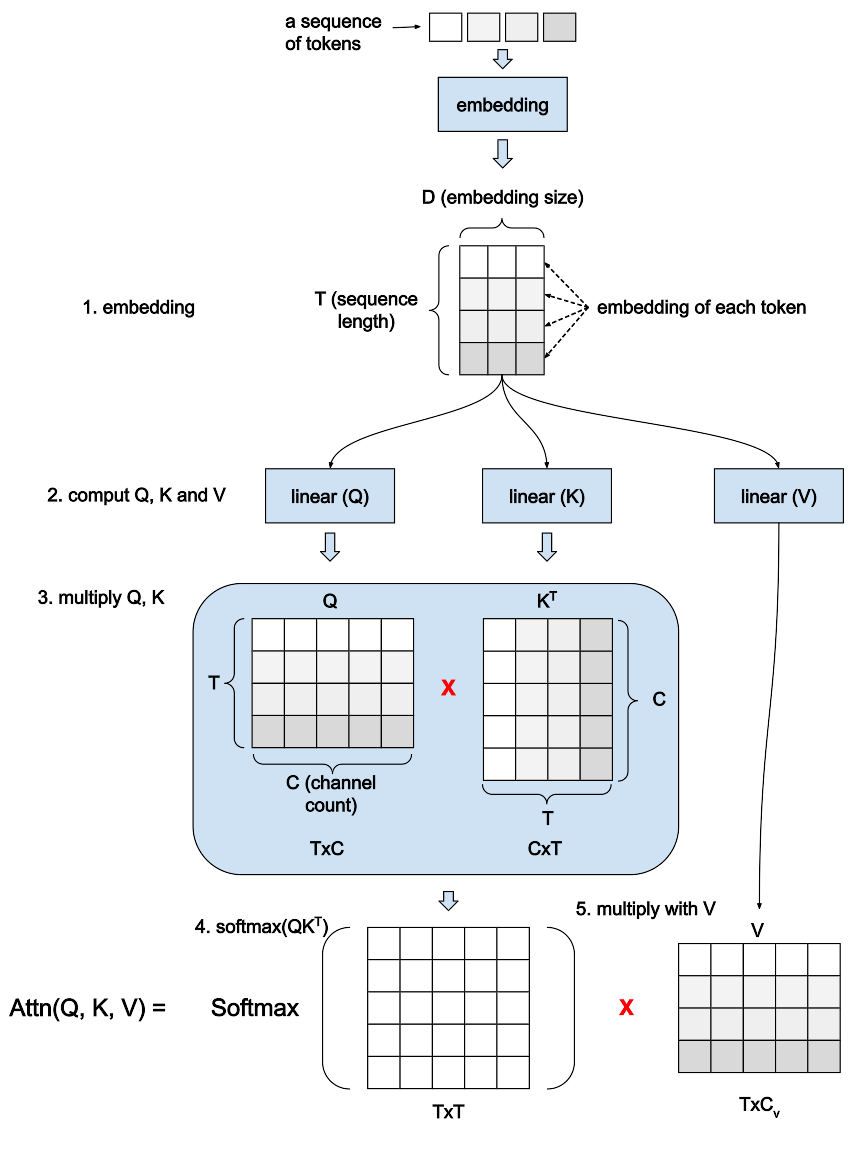
1. The input (sequence of tokens) is turned into a sequence of embeddings through the embedding layer. Each embedding is a vector size of D, and if the sequence length is T, we’ll have T vectors each of size D. This is why the output of the embedding layer is a TxD matrix.
2. The embeddings of the input are then fed into three linear layers, which transform it into three matrices Q, K and V. Similarly, each row of the matrix is a vector corresponding to one token (position) in the input sequence. The size of the vector is called “channel”, which is denoted as C here. Both Q, K matrices are of shape TxC. The V matrix must have T rows, but the size of each vector could be different than Q and K. For ease of discussion, we assume V is also in shape of TxC.
3. Multiply the Q and K matrices. To make this possible, we must first transpose the K matrix to make it in CxT shape. Then multiplying a TxC matrix with a CxT matrix will give us a TxT matrix. What does this TxT matrix mean? Remember that each row in Q and K corresponds to one token (position) in the input sequence. So multiplying Q and K means we let every token in the sequence “interact” with every token. In the resulting TxT matrix, the value at row i and column j is the result of interaction between the i-th token and j-th token.
4. Next we’ll do a softmax on this TxT matrix. The softmax function takes a vector (list of values) as input, and outputs a vector of the same size. Each item in its output vector is a positive value that describes the “distribution” or “probability” of the corresponding item in the input. Again, please be noted that we omit the scaling part in the original Self Attention equation for brevity.

In this definition, \(softmax_j\) gives you the distribution/probability of the j-th item. Since there are T items, the entire softmax function will give you a vector size of T.

So how does this work on a matrix? It’s simple - you apply softmax to each row of the matrix (each being a vector size of T). Since the matrix is TxT, the resulting matrix is also TxT.

1. The last step is to multiply the TxT matrix with V, which is assumed to be a TxC matrix, and the result will also be a TxC matrix. My understanding is that \(softmax(QK^T)\) tells the attention between every token pair in the sequence, and V works like a “gate” to filter out those insignificant interactions.

Now how do these steps map to the iterative form of the Self Attention equation?

Let’s take a closer look at the TxT matrix from step 3 (multiply Q and K).

Each row of this \(QK^T\) matrix has T values. From the definition of matrix multiplication, the i-th value in row t is the product of t-th row of Q and i-th column of K, which can be denoted as dot product of \(Q_t\) and \(K_i\). So the \(QK^T\) matrix will look like this:

Then in step 4, we run softmax on each row of this matrix. Suppose we are running softmax on row t. According to the definition of softmax, the result should look like this:

Here \(S_t = \sum_{i=1}^T e^{Q_t \cdot K_i}\) is the sum of the row t. So the matrix after softmax will look like this:

So for row t, softmax gives us a vector of T values. The j-th value of row t can be expressed like this:

Now let’s do step 5, multiply the softmax output with V.

For ease of discussion, let’s denote the softmax value at row t and column j to be \(M_{t,j}\). So what we are trying to do is:

Looking at row t of the resulting matrix, the j-th column would be:

So the values in row t will look like this:

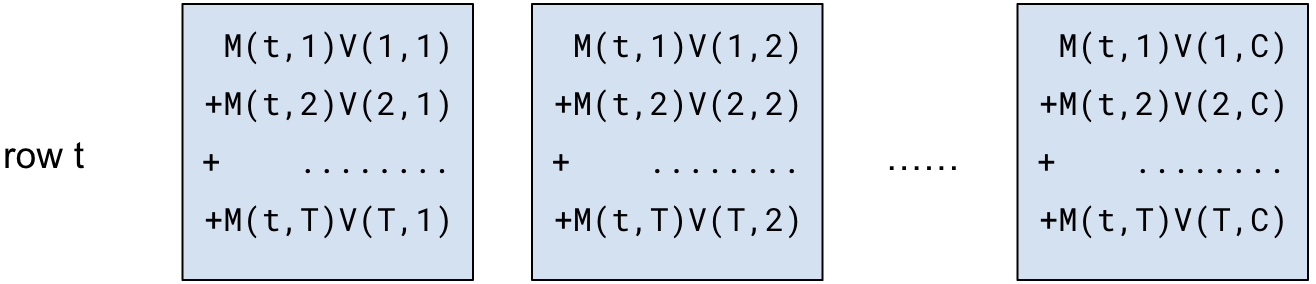
Remember V is a TxC matrix, so V(i) (the i-th row of V) is a vector of size C: V(i,1), V(i,2), ... V(i,C). So we can do a little reorganization and transform the expression as follows:

So the values in row t can be expressed as a weighted sum of every vectors in V.

And because \(M_{t,j}\) is denoted as:

Put this back into the equation above:

This is the iterative form of the Self Attention equation.

So what did we learn? We started from the basics of Self Attention, went through every step of the computation and figured out how we map the equation’s matrix form into its iterative form. This is particularly useful if you would like to compare it with other RNN-like algorithms (in fact, I went through this when I studied the RWKV algorithm). I decided to write down my journey so I can revisit it some time, and I hope it will be somewhat helpful to you as well.